Notes de TD:
TD1 Enveloppes Convexes
TD1 en faire plus
TD2 Triangulation de Delaunay
Vous pouvez commencer par charger le programme initial et le compiler. Actuellement,
La triangulation et le dernier point saisi (clic droit) sont affiche's apre`s chaque clic.
Vous aurez besoin de la documentation CGAL.
- 1. Modifier le programme pour que le bouton de droite provoque en plus de l'affichage du point saisi en bleu, celui de son plus proche voisin dans les sommets de Delaunay en vert.
- 2. Modifier le programme pour que le bouton du milieu provoque l'affichage en orange du triangle contenant le point clique' et de son cercle circonscrit en noir.
- 3. Modifier le programme pour que l'inte'rieur des triangles soit colorie's en rouge pale si le rapport (aire du triangle / aire du cercle circonscrit) est infe'rieur a` 0.3 et en vert pale sinon.
- 4. Lors du clic droit, afficher en plus tous les triangles incidents au plus proche voisin du point clique en bleu.
- 5. Lors du clic droit, afficher tous les triangles traverse's par la droite horizontale passant par le point clique en bleu.
- 6. En circulant autour du sommet infini, calculer et faire afficher en noir l'enveloppe convexe de l'ensemble des points de la triangulation.
Des liens plus rapides vers ce dont vous avez besoin dans la librairie CGAL
- Vous aurez besoin de la documentation CGAL.
- La triangulation est là avec les fonctions d'accés comme "locate"
- les trucs spécial pour Delaunay comme par example "nearest_neighbor" vont être là
- la géométrie est donnée dans la "geometric traits", on utilisera à cette place le "Kernel" définit là
- la structure de données est dans la "triangulation data structure" décrite là
- celle ci est elle même construites à partir de faces là
- et de sommets là
- les couleurs sont là
Modifier le programme pour qu'a chaque fois que l'on clique sur le bouton du milieu on e'nume`re les voisins du point bleu dans la triangulation :
premier clic, le plus proche voisin,
deuxie`me clic, le deuxie`me plus proche voisin,
troisie`me clic, le troisie`me plus proche voisin,
....
class Dist_order {
const Delaunay *t;
const Point *p;
public:
Dist_order(const Delaunay *tr, Point *po)
: t(tr), p(po) {}
bool operator()(const VertexH v1, const VertexH v2) const
{
return (CGAL::compare_distance_to_point(*p,v1->point(),v2->point()) == CGAL:
:SMALLER );
}
};
typedef std::set
TD3/4 : Problèmes de robustesse
Les programmes fournis en dimension 2 et dimension 3 plantent pour un nombre de points assez grands.
- changer float en double et constater que l'on peut mettre plus de points.
- faire un exemple plus méchant en insérant d'abord une boite englobante, puis des points aleatoires sur un segment de droite (une portion de plan), et constater que ça plante même en double.
- utiliser un type de nombre exact, par exemple des Quotient de MP_float (doc).
- utiliser le noyau filtré (doc).
- comparer les temps d'exécution de ces différentes solutions dans le cas difficile, dans un cas facile (points random).
correction en dim 2 et correction en dim 3
Sujet 1 : Benchs avec différents ordres d'insertion
- Engendrer dans un tableau N points aléatoires dans un carré.
- Construire une première triangulation de Delaunay en insérant ces points dans l'ordre (aléatoire) du tableau.
- Recommencer après avoir trié le tableau en x
- Engendrer dans un tableau N points sur la spirale t*(cos(t), sin(t)) pour t dans [0,10.Pi].
- Construire une triangulation de Delaunay en insérant ces points dans l'ordre la spirale (intérieur vers extérieur).
- Recommencer dans l'ordre inverse
- Recommencer avec des points aléatoires sur la spirale.
Vous pourrez débuter avec le squelette
Sujet 2 : Delaunay tridimensionnel
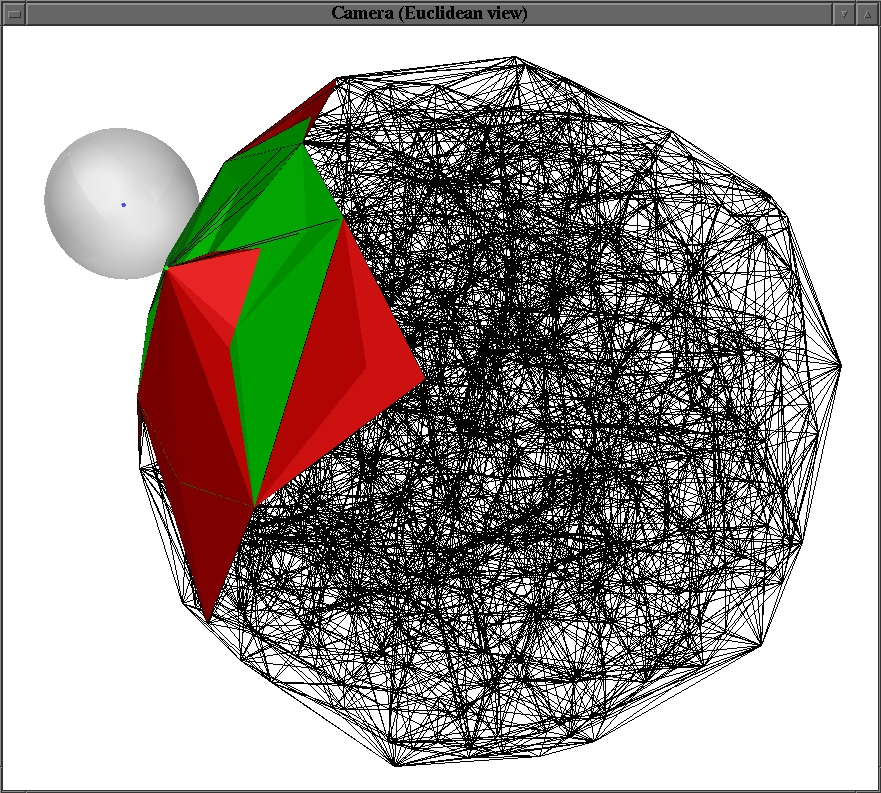
Vous pouvez commencer par charger le programme initial. Le programme initial engendre une liste de points en 3D, calcule la triangulation de Delaunay et l'affiche dans "Geomview". Puis il permet de saisir un point à la souris, affiche ses coordonnées et le dessine en bleu.- Modifier le programme pour qu'il génère une liste de points aléatoires à l'intérieur de la sphère unité.
- Modifier le programme pour qu'il affiche l'enveloppe convexe des points. Cette dernière peut être envoyée au Geomview_stream sous la forme d'une liste de triangles.
- Effacer, et réafficher la triangulation de Delaunay.
- Saisir un point à l'aide d'un pickplane, comme dans le programme initial.
- Afficher en vert le sommet de la triangulation le plus proche du point saisi. On affichera également la sphère centrée en ce point passant par le point vert.
- Modifier le programme pour qu'il affiche également le bord de l'étoile du point vert.
- Modifier le programme pour qu'il affiche également le bord de la zone de conflit du point saisi.
Pour la soutenance, vous ferez une demonstration de vos differents programmes.
Voici le genre de résultat que vous devriez obtenir :