10:00 - 10:15
Welcome
10:15 - 11:45
Presentations
10:15 - 10:45
CGAL 3D Triangulations in Periodic Spaces
Manuel Caroli and Monique Teillaud, INRIA
slides
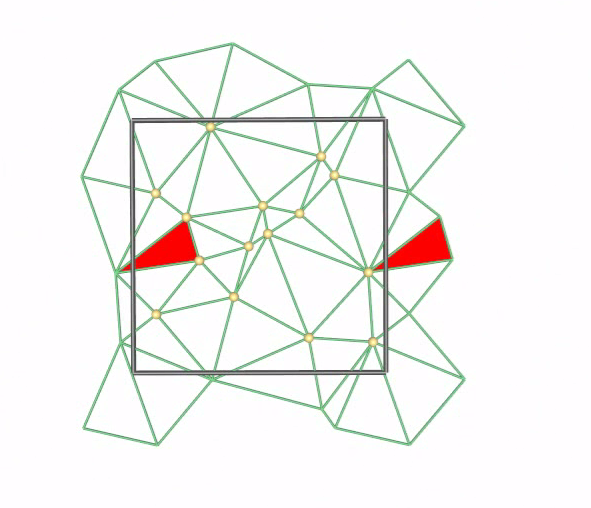
In this talk we present the implementation of periodic 3D Delaunay
triangulations in CGAL, the Computational Geometry Algorithms Library.
Naively extending the Delaunay triangulation algorithm to periodic triangulations would require to compute a triangulation of infinitely many points. However, exploiting the periodicity it is possible to compute a triangulation using only a finite number of periodic copies of each input point. We describe how we handle this issue using even only one periodic copy of each point, whenever this is possible. We formulate a condition on the point set that is efficiently verified by our implementation. Additionally we provide some heuristics for speed-up.
To the best of our knowledge there is no implementation available using this approach. Unlike other available implementations we came to know about we guarantee to correctly/exactly compute the periodic Delaunay triangulation for a point set without having the need of any special boundary treatment.
For topological reasons the interface requires some changes, however we maintain a maximum part of the interface of the CGAL 3D Triangulation package.
A video about this software is available
here
(the image on the right illustrates the 2D case).
To know more
10:45 - 11:15
Periodicity and the Design of Bone Scaffolds
Maarten Moesen, Jan Schrooten, and Stepan V. Lomov, Department of Metallurgy and Materials Engineering (MTM), K.U. Leuven
Bone scaffolds are porous materials used for replacing damaged bone in
therapies for healing bone defects up to a few centimeters. To enhance
bone regeneration, bone scaffolds should provide various biological,
transport, and mechanical functions. The general aim of this work is
to support these functions by controlling biomechanically related
material properties throughout a bone scaffold via an appropriate
design of its structure and geometry.
One design strategy involves constructing a regular bone scaffold based on a parametric unit cell. Because such a unit cell provides a complete geometrical description of the bone scaffold while being relatively small, it allows cost-effective determination of local and apparent material properties using numerical simulations, on the condition that appropriate boundary conditions are applied. In this talk, the suitability of periodic boundary conditions will be discussed, together with the practical requirements that they impose on mesh generation. In addition, open questions will be raised concerning the characterization of topological properties based on periodic unit cells.

11:15 - 11:45
Multi-scale mechanics of granular materials
O. Duran, N.P. Kruyt, K. Bertoldi and S. Luding,
Department of Mechanical Engineering, University of Twente
Granular materials consist of nearly-rigid, interacting particles and
voids. The objective of multi-scale mechanics of granular materials is
to study the relation between particle properties at the micro-scale
and continuum-mechanical properties at the macro-scale, such as the
average stress and strain tensors.
To obtain detailed information at the micro-scale, Discrete Element Method simulations are frequently used, in which the motion of a large set of particles is determined by numerically integrating the equations of motion. To suppress wall effects and to maintain spatially homogeneous deformation, such simulations are often performed in three-dimensional periodic space.
To study characteristics and statistics of the deformation at the micro-scale, Delaunay tessellations are used. In addition, adaptive multi-phase computational fluid dynamics methods, with hierarchical data-structures, are being developed that depend on fast Delaunay tessellations.

12:00 - 13:30
Lunch
13:30 - 14:30
Presentations
13:30 - 14:00
Periodic Computer Representations of the Cosmic Structure
Rien van de Weijgaert, Kapteyn Institute, University of Groningen
slides(ppt, 80 Mb)
Cosmology is the study of the structure and evolution of the Universe
and its contents. One of the most important issues is the formation
of structure and the emergence of cosmic objects out of the almost
featureless pristine Universe some 13.6 Gyrs ago. All evidence points
towards a gravitational amplification of initial Gaussian density and
velocity ripples with tiny amplitudes. An important consideration
is that of the cosmological principle: there are no preferred or
central positions in the Universe, each sizeable volume of the
Universe is more or less (statistically) representative.
When simulating the evolution of cosmic structure we therefore need to guarantee that the simulation volume is representative. This is most straightforwardly accomplished by specifying volumes with periodic boundary conditions. Effectively it means that the simulation ignores the influence of primordial density and velocity fluctuations with wavenumbers smaller than the fundamental wavelength of the simulation box.
One of the main instruments for studying the formation of structure
are N-body simulations, in which the cosmic mass distribution is
reflected in a representative spatial distribution of discrete particles.
I will describe how Delaunay and Voronoi tessellations are powerful
instruments for analyzing and following the multiscale and strongly
patterned nature of spatial structure on Megaparsec scales.
(image processed from images made my Miguel Aragon-Calvo)

14:00 - 14:30
Radiative Transfer Using Unstructured Grids
Cornelis Dullemond, Max-Planck-Institut for Astronomy, Heidelberg
slides
Arguably, two of the most fundamental problems in astrophysics are the
motion and flow of gas ("hydrodynamics") and the propagation of
radiation through these structures of gas ("radiative transfer").
Since in problems of cosmology, star formation, galaxy formation etc,
the flows of interstellar gas are very chaotic and clumpy, theoretical
modelers have since long used "adaptive mesh refinement" (AMR)
techniques to assure sufficient resolution at places where this is
necessary while reducing the spatial resolution there where little gas
is present.
However, it has become clear that traditional hierarchical AMR techniques have many problems, and slowly but surely the astrophysical community is getting used to the idea of using fully unstructured grids to model complex astrophysical problems. Since space is effectively infinite, to limit the computational domain to finite size for hydrodynamic calculations, periodic boundary conditions are often invoked. While they are not necessarily realistic, they appear to be much less troubling than fixed wall or outflow boundary conditions. To perform the corresponding radiative transfer for such simulations requires that also the radiative transfer model can make use of such boundary conditions. In particular for cosmological simulations this is of particular use.
I will mainly present how radiative transfer is done or will be done on Delaunay and/or Voronoi grids, and I will then briefly outline the pros and cons of using periodic boundary conditions for this problem.

14:30 - 15:00
Coffee Break
15:00 - 16:45
Discussion
The format of this session is open, in the sense that it allows to build
working groups in order to learn from each other, identify common problems, etc.
16:45 - 17:00
Closing