
Geometric problems are central in many areas of science and
engineering. Computational geometry, the study of combinatorial and
algorithmic problems in a geometric setting, has tremendous practical
applications in areas such as computer graphics, computer vision and
imaging, scientific visualization, geographic information systems,...
Traditionally, the scope of computational geometry research has been
limited to manipulation of geometric elements in the Euclidean space
Rd.
| Due to the recent emergence of standardized software libraries, in particular the Computational Geometry Algorithms Library CGAL, developed in the framework of an Open Source Project, the so-far mostly theoretical results developed in computational geometry are being used and extended for practical use like never before. |  |
|
|
Related Events
Structures on Surfaces, CIRM, Marseille, May 2 - 6, 2022 Astonishing workshop, LORIA, Nancy, September 25-26, 2017 Geometric Aspects of Materials Science, Brisbane, Australia, July 4-5, 2017 Workshop on Computational geometry in non-Euclidean spaces, INRIA, LORIA, Nancy, August 26--28, 2015 Workshop on Geometric Structures with Symmetry and Periodicity, Kyoto University, Japan, June 8-9, 2014 OrbiCG/Triangles Workshop on Computational Geometry, INRIA Sophia Antipolis - Méditerranée, 8 - 10 Dec 2010 Subdivide and Tile: Triangulating spaces for understanding the world (program), Lorentz Center, Leiden, The Netherlands, 16 - 20 Nov 2009 CGAL Prospective Workshop on Geometric Computing in Periodic Spaces, INRIA Sophia Antipolis - Méditerranée, 20 October 2008
This work has been partially supported by
|
| Delaunay Triangulations of Closed Euclidean Manifolds | |

(image by Manuel Caroli - larger version) |
Flat torus with square fundamental domain
|
|
Periodic Meshes |
|
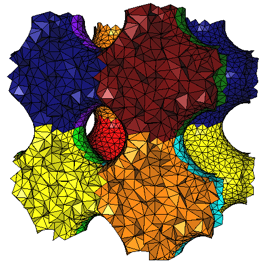
(internship of Mikhail Bogdanov) |
|
| Delaunay Complexes in Hyperbolic Spaces | |
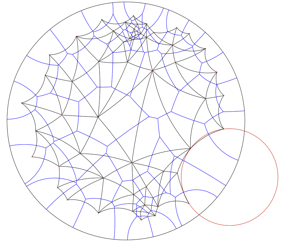
|
|
|
Delaunay Triangulations of Closed Hyperbolic Surfaces |
|
Bolza surface (genus 2)
|

(internship of Mathieu Schmitt) [RR 8179] |
| Delaunay Triangulations of the Sphere | |
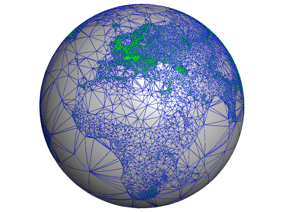 
|
(work started during the internship of Olivier Rouiller and improved during the internship of Claudia Werner) |
|
Triangulations of the Projective Plane |
|
|
[MACIS'07] (work done during the internship of Mridul Aanjaneya) |