Master internship: Flipping triangulations of hyperbolic surfaces

Supervision and Contact: Vincent Despré and Monique Teillaud
Location: Gamble group, INRIA Nancy - Grand Est, LORIA

The work may extend to a PhD on a related topic.

Context

In the Euclidean plane, the Delaunay triangulation of a set of n points P is the unique (when P is non-degenerate) triangulation with vertex set P for which the circumdisk of each triangle does not contain any point of P in its interior. It has many applications and has been extensively studied [BCKO].
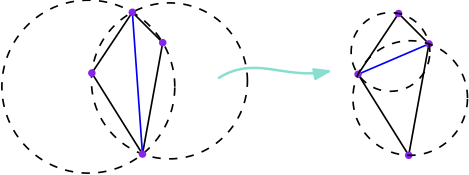
When a general (non-Delaunay) triangulation is given a sequence of edge flips allows to compute the Delaunay triangulation.

We are interested by the generalization of the Delaunay triangulations on surfaces of genus > 1. Such a surface is a hyperbolic surface, which can be seen as the quotient of the hyperbolic plane under the action of a discrete group of hyperbolic isometries [MT]. The flip algorithm has a complexity O(f(T).n²), where f(T) is an explicit measure of the quality of the input triangulation T [DST]. This measure f(T) is not proven to be tight.

Goal of the internship

The twofold objectives are to propose optimizations to the flip algorihms in theory as well as in practice. To this aim, the student will first need to deeply understand the mathematical aspects of the algorithm on hyperbolic surfaces. (S)he will study the possibility to propose better measures of the quality of the input triangulation. (S)he will also implement the algorithm in C++ and propose heuristic improvements.

Required skills

- Groups, topology, geometry,
- Algorithms design and analysis,
- Basic skills in C++.

References

[BCKO] M. de Berg, O. Cheong, M. van Kreveld and M. Overmars. Computational Geometry: Algorithms and Applications. Springer-Verlag, 2008.
[DST] Vincent Despré, Jean-Marc Schlenker, and Monique Teillaud. Flipping Geometric Triangulations on Surfaces. 36th Symposium on Computational Geometry, 2020.
[HNU] F. Hurtado, M. Noy, and J. Urrutia. Flipping edges in triangulations. Discrete & Computational Geometry, 22(3):333-346, 1999.
[MT] B. Mohar and C. Thomassen. Graphs on Surfaces. Johns Hopkins University Press, 2001.