Supervision and Contact:
Vincent Despré
and
Monique Teillaud
Location:
Gamble group, INRIA Nancy - Grand Est,
LORIA
Context
Delaunay triangulations in the Euclidean space Rd have been
extensively studied [1]. Their mathematical properties are well
understood, many algorithms to construct them have been proposed and
analyzed.
The following simple incremental algorithm [2] allows for very
efficient implementations:
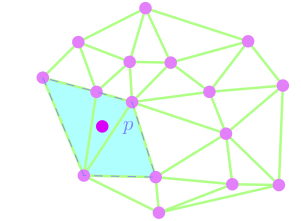
For each new point p
- Find the simplices in conflict with p, i.e. the simplices
whose circumscribing ball containts p
- Remove these simplices from the triangulation. This creates a hole.
- Fill the conflict hole by ``starring'' it from p.


Periodic structures are arising in many fields, ranging from
(nano-)materials to astrophysics. Modeling such periodic structures
can be achieved through the use of Delaunay triangulations of the flat
torus, which is homeomorphic to the quotient of Rd under
the action of a group of translations.
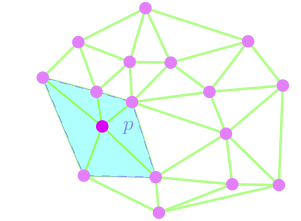
An algorithm was proposed for general closed flat manifolds,
i.e. compact quotient spaces of the Euclidean space under the action of a discrete
group of isometries [3]. The algorithm is based on the abovementioned
incremental algorithm, which subsumes that that the
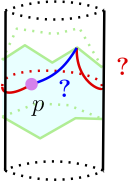
conflict hole is a topological disk for any new point p. This
is a priori not always the case on a surface:
Topic
A variant [7,1] of the incremental algorithm works as follows in
R2:
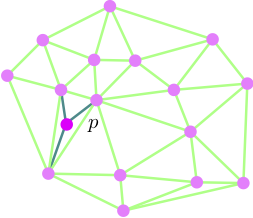
For each new point p
- Split the triangle containing p into three triangles
- Flip non-Delaunay edges
- Propagate flips until there are no more non-Delaunay edges.
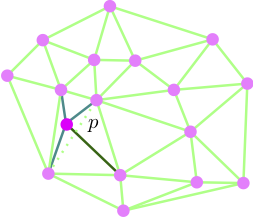
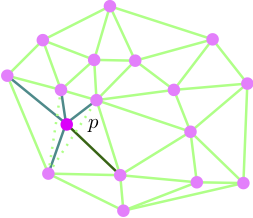
The question to study is whether this variant extends to the
flat torus in 2D and 3D and still works when there
are loops or double edges in the triangulation.
The question will be studied theoretically and may be completed by a
prototype implementation.
The work may extend to a PhD on a related topic.
References
[1]
Mark de Berg, Otfried Cheong, Marc van Kreveld, and Marc Overmars.
Computational Geometry - Algorithms and Applications,
Springer-Verlag.
[2]
Adrian Bowyer. Computing Dirichlet tessellations. The Computer Journal, 24:162-166, 1981.
[3]
Manuel Caroli and Monique Teillaud.
Delaunay triangulations of closed Euclidean d-orbifolds,
Discrete and Computational Geometry, 55(4):827-853, 2016.
[4]
Nico Kruithof.
2D periodic triangulations
[5]
Manuel Caroli, Aymeric Pellé, Mael Rouxel-Labbé, and Monique Teillaud.
3D periodic triangulations
[6]
Johan Hidding, Rien van de Weygaert, Gert Vegter, Bernard J.T. Jones, and Monique Teillaud.
Video: The Sticky Geometry of the Cosmic Web,
Proceedings 28th Annual Symposium on Computational Geometry, pages 421-422, 2012.
[7]
Charles L.Lawson. Software for C1 Surface Interpolation. C. L. Lawson. Technical report. Jet Propulsion Laboratory. 1977.
[8]
Herbert Edelsbrunner and N.H. Shah.
Incremental topological flipping works for regular triangulations.
Algorithmica, 15:223-241, 1996.