Sujet de stage proposé de BAC+4 à BAC+5, conjointement avec Dmitry Sokolov.
Présentation générale du domaine
En informatique, on représente souvent les objets géométriques par des maillages. En particulier, les volumes sont en général représentés par des maillages composés de tétraèdres, car leur génération et leur manipulation sont assez bien maîtrisées. Néanmoins, certaines simulations numériques préfèrent travailler avec des hexaèdres (petits cubes déformés), ce qui pose le problème de convertir des maillages tetraédriques en maillage hexaédriques. Ce problème est extrêmement complexe du fait des contraintes combinatoires fortes auxquelles sont soumis les maillages hexaédraux (contrairement aux maillages tetraédraux). Nous cherchons à résoudre ce problème en plaçant une grille déformée à l’intérieur du volume, qui peut éventuellement se recoller sur elle-même, et qui doit être alignée avec le bord du volume.
Actuellement, le positionnement de la grille est réalisé par deux optimisations numériques successives: la première définit l’orientation (Frame Field) des arêtes de la grille déformée [1], puis la seconde positionne la grille en respectant au mieux l’orientation trouvée à l’étape précédente [2]. Actuellement, les Frame Fields sont générés en minimisant leur courbure. Cette heuristique est globalement satisfaisante, mais nous souhaitons aller plus loin, en y intégrant des contraintes induites par la seconde étape.
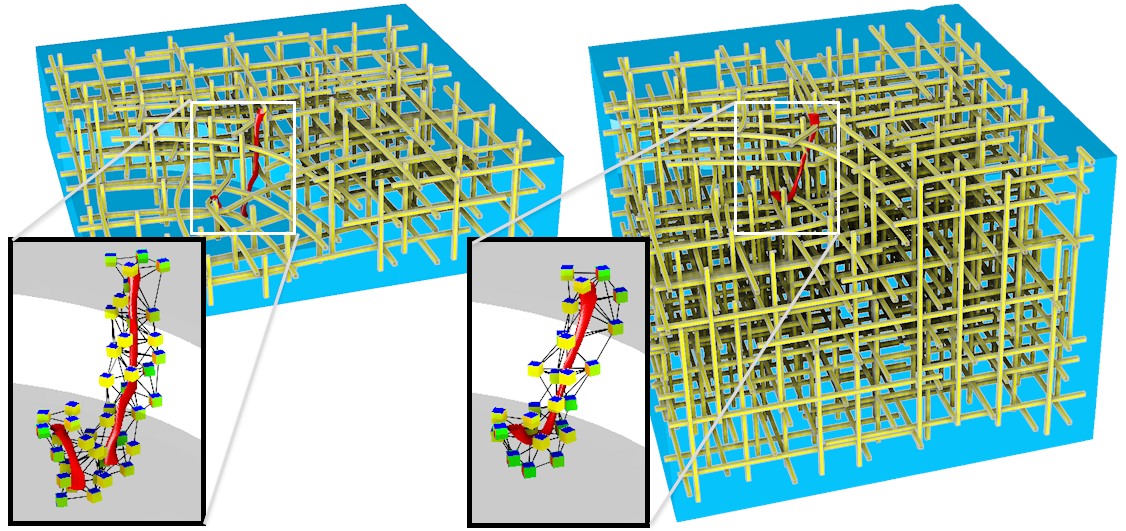
Un Frame Field associe à chaque point de l’espace trois directions orthogonales entre elles, représentées ici par les courbes jaunes à section carrée. Les singularité (en rouge) sont des courbes autour desquelles le Frame Field réalise une permutation d’axes. Celles du modèle de gauches sont alignées avec l’une des direction du Frame Field, ce qui les rends (localement) compatible avec un remaillage hexaédral, et qui n’est pas le cas pour le modèle de droite.
Objectifs du stage
Les singularités d’un Frame Field 2D sont simples à caractériser: un point est singulier si l’intégrale de la rotation du champ le long du bord d’un voisinage (infiniment petit) de ce point n’est pas nulle. Pour le remaillage quadrangulaire (petits carrés déformés), cela implique la présence d’un sommet irrégulier i.e. de valence différente de 4. Cette caractérisation ne s’étend malheureusement pas au cas volumique car l’intégration des rotations 3D est mal définie. Cependant, nous savons que les seules courbes de singularité qui correspondent à un remaillage hexaèdre sont des singularités 2D « extrudées » selon la troisième direction: elles peuvent devenir des arêtes partagées par un nombre d’hexaèdres différent de 4.
Lorsque l’on se contente de trouver le Frame Field de courbure minimale, d’autres types de singularité apparaissent (voir la partie droite de l’image). L’idée de ce stage est de décomposer le calcul du Frame Field en deux étapes: la première va définir une direction stable, et la seconde va calculer les deux autres directions. La direction stable peut être imposée par le modèle, comme c’est le cas en géologie avec la normale aux strates géologiques, mais elle pourra aussi être définie automatiquement par une heuristique. Nous essayerons par exemple de prendre la direction de moindre courbure dans un Frame Field de courbure minimale ce qui, dans le cas de l’image, sera tout simplement la hauteur. Les deux autres directions devront être calculées en s’inspirant des algorithmes de génération de Frame Field 2D, mais en imposant que le champ reste constant le long des lignes de flux de la direction stable. Pour imposer ces contraintes dans l’optimisation numérique du champ de direction, il faudra remplacer certaines variables par des combinaisons linéaires d’autres variables. Intuitivement, les variables liées à un sommet S seront exprimées comme combinaison linéaires des variables associées aux coins d’un triangle traversé par la ligne de flux passant par ce sommet $S$. Ce travail s’inscrit dans la continuité de [1], et qui est une référence qui présente les algorithmes que nous utilisons actuellement pour générer les Frame Fields 2D et 3D.\\
Références bibliographiques:
[1] Ray Nicolas, Sokolov Dmitry, Lévy Bruno. Practical 3D Frame Field Generation. ACM TOG 2016.
[2] Sokolov Dmitry, Ray Nicolas, Untereiner Lionel, Lévy, Bruno. Hexahedral-Dominant Meshing. ACM TOG 2016.
Compétences espérées:
La principale qualité attendue est l’envie d’apprendre et de travailler en équipe. Il n’est pas nécessaire d’avoir un niveau exceptionnel en mathématique, mais une bonne intuition géométrique en $3D$ sera un plus. Être à l’aise en programmation sera nécessaire pour pouvoir tester différentes idées. Notre base de code est en C++, mais les difficultés seront principalement d’ordre algorithmiques (ni syntaxiques, ni architecturales).



