Formulation Éléments finis pour les Paramétrisations Globales Périodiques

proposé avec Laurent Alonso à des étudiants en cursus math appli à BAC+4/5

Présentation générale du domaine:

En informatique, les surfaces sont généralement représentées par des maillages triangulés car ces derniers sont faciles à générer, à éditer et à afficher. Cependant, pour évaluer des propriété différentielles (dérivées, courbure, etc.) ou représenter des champs (scalaires vectoriels, etc.) sur la surface, il est préférable d’utiliser une représentation paramétrique (e.g. splines) dans laquelle la surface est une partie de l’image d’une fonction continue de f:R² ← R³. On peut bénéficier des avantages des deux représentations en munissant une surface triangulée d’un domaine paramétrique. Pour ce faire, un algorithme dit de paramétrisation va définir pour chaque triangle sa pré-image dans ². Classiquement, ces algorithmes préservent les adjacences des triangles dans le domaine paramétrique, ce qui limite leur utilisation à une petite classe de surfaces (disque topologique avec faible courbure Gaussienne). Afin de traiter d’avantage de surfaces, nous acceptons que la fonction inverse possède un certain type de discontinuité (conservation de grille), qui n’impacteront pas certaines applications telles que le remaillage en quadrangles [3] ou le stockage de couleur sans coutures apparentes [4].

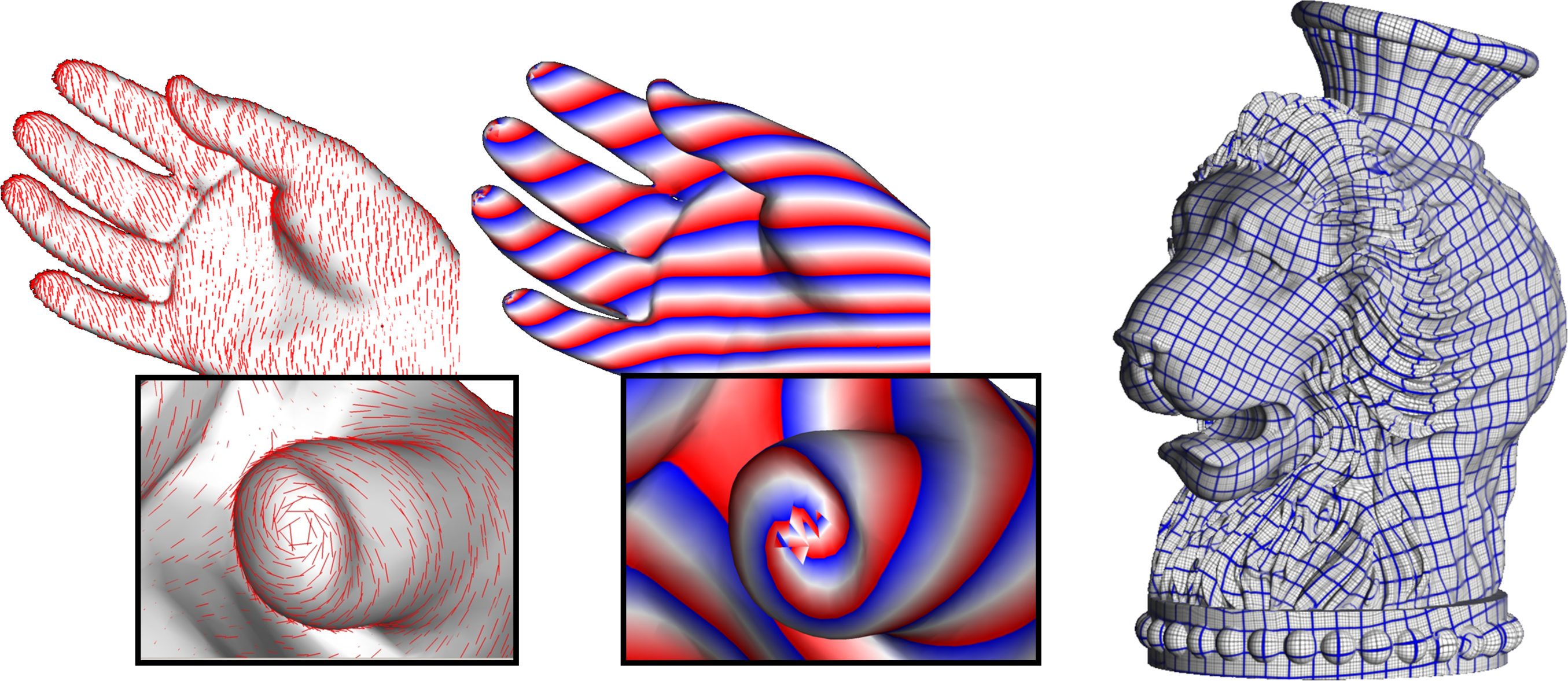
La première étape définit un champ de vecteur (à gauche), puis la seconde intègre ce champs (au milieu). On remarque sur les zooms du pouce que la discrétisation ne permet pas de capturer correctement les singularités. En pratique, quatre champs de vecteurs inter-connectés sont intégrés simultanément pour obtenir la paramétrisation globale (à droite).}

Objectifs du stage:

La génération de paramétrisation globale (avec discontinuité) fonctionne en deux étapes (voir [2] et la Figure): la génération d’un champ de direction, puis l’intégration de ce champ de direction. Pour la première étape, le problème est équivalent à minimiser le carré de la variation d’angle d’un champ de vecteur unitaire tangent à la surface. Il s’agirait d’un simple problème de Dirichlet s’il n’y avait pas la contrainte de norme unitaire sur les vecteurs. Malheureusement, dans le cas continu, cette contrainte fait diverger la fonction objectif près des singularités du champ, or ces dernières sont nécessaires pour un grand nombre de surfaces (théorème de la boule chevelue, théorème de Poincaré-Hopf). Une solution pragmatique est de ne considérer l’énergie que le long des arêtes du maillage, ce qui fait sortir les singularités du domaine d’intégration (elles seront à l’intérieur des triangles). Cette solution fonctionne relativement bien [2], mais rend le processus fortement dépendant du maillage, et non pas seulement de la géométrie de la surface. Récemment, Beaufort et al [1] ont proposé une discrétisation par éléments finis de la formulation continue qui est beaucoup plus forte d’un point de vue théorique. Leur approche s’inspire la théorie de Ginzburg-Landau, initialement introduite pour définir les vortex dans les champs magnétiques.

Étant donné que la seconde étape (intégration du champs) requiert l’optimisation d’une fonction dont l’expression est extrêmement similaire à la première, nous pourrons probablement la traiter avec une approche semblable. Le travail consistera donc à bien comprendre les travaux de lissage de champs de vecteurs unitaires, et à les transposer (en ajoutant un terme à droite) au cas de la paramétrisation globale. Cette formulation continue permettrait de replacer le problème de la paramétrisation globale dans un cadre plus rigoureux, dans lequel on pourrait sans doute obtenir de meilleurs résultats.\\

Références bibliographiques:

[1] Pierre-Alexandre Beaufort, Jonathan Lambrechts, François Henrotte, Christophe Geuzaine, Jean-François Remacle. Computing cross fields – A PDE approach based on the Ginzburg-Landau theory. arXiv:1706.01344
[2] Nicolas Ray, Wan Chiu Li, Bruno Lévy, Alla Sheffer, Pierre Alliez. Periodic Global Parameterization. ACM TOG 2006.
[3] Felix Kälberer Matthias Nieser Konrad Polthier. QuadCover – Surface Parameterization using Branched Coverings. octobre 2007.
[4] Ray Nicolas, Nivoliers Vincent, Lefebvre Sylvain, Lévy, Bruno. Invisible Seams. EGSR 2010.

Compétences espérées:
La principale qualité attendue est l’envie d’apprendre et de travailler en équipe. D’autre part, il sera nécessaire d’être suffisamment à l’aise en mathématique et en informatique pour comprendre [1] et l’implanter. Le code devrait être assez simple puisqu’il s’agit essentiellement de construire les matrices et les vecteurs correspondants à la discrétisation du problème. Le choix du langage de programmation est libre, mais je suggérerais par défaut du C++ ou du python.