Résumé : Ce rapport décrit l'algorithme utilisé par le programme epelle et son implantation dans le langage C. Ce programme permet de vérifier plus de 30000 mots par seconde sur une station de travail, avec un taux d'erreur nul, contrairement aux méthodes de hachage utilisées par spell. Le principe est d'utiliser des arbres digitaux, ce qui permet aussi un gain en espace par rapport à la liste de mots (de l'ordre de 5 pour le dictionnaire français). La création de l'arbre digital correspondant au dictionnaire français (près de 240000 mots) ne dure qu'une dizaine de secondes. Le même programme est directement utilisable pour d'autres langues, et même pour n'importe quelle liste de mots alphanumériques.

1  Utilisation du hachage

for i := 0 to N-1
   T[i] ¬ false
foreach m Î D
   T[f(m) modN] ¬ true

% cat dico
auto
autobus
camion
train
voiture
% /usr/lib/spell/hashmake < dico | tee dico.codes
454524372
647545412
460442120
417177515
323215174

% /usr/lib/spell/spellin 5 < dico.codes > dico.hash
spellin: expected code widths = 26.146019
spellin: 5 items, 0 ignored, 0 extra, 5 words occupied
spellin: 32.000000 table bits/item, 3315.200000 table+index bits

% cat texte
autobu
velo
auto
voiture
% spell -d dico.hash < texte
autobu
velo
voiture

2  Utilisation d'arbres digitaux

---

Figure 1 : L'arbre digital n-aire du dictionnaire auto, autobus, avion, bus, camion.

---

---

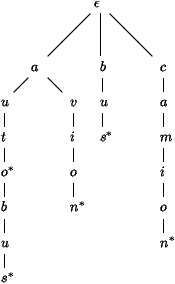
Figure 2 : L'arbre digital binaire du dictionnaire auto, autobus, avion, bus, camion.

---

Algorithme recherche(s₁ ... s_l).
{ renvoie true si le mot est dans le dictionnaire, false sinon }
   i ¬ 1    { indice de la lettre à chercher }
   t ¬ racine de l'arbre digital
   tant que i £ l
      tant que lettre(t) ¹ s_i
         si t n'a pas de fils droit, renvoyer false, sinon t ¬ fils droit de t
      si i=l, renvoyer booléen(t), sinon i ¬ i+1

---

Figure 3 : L'arbre digital compressé du dictionnaire auto, autobus, avion, bus, camion.

---

Algorithme compactifie(t).
{ renvoie l'entier associé à l'arbre t }
   si t est vide, alors renvoyer 0
   j ¬ compactifie(t_gauche)
   k ¬ compactifie(t_droit)
   i ¬ cherche(j,k,t_car,t_bool)
   si i < 0 alors i ¬ cree(j,k,t_car,t_bool)
   renvoyer i

3  Le dictionnaire français

4  Quelques résultats

---

langue	mots	taille	noeuds avant	noeuds après	taille	temps de création
		dico	compression	compression	table	(HP 9000/700)
allemand	160087	2.1Mo	499699	150839	0.9Mo	15s
anglais	51899	0.5Mo	130155	43174	0.3Mo	2.6s
français	239211	2.6Mo	523703	84286	0.5Mo	12s
hollandais	148602	1.7Mo	427882	106648	0.6Mo	8.8s
italien	60541	0.6Mo	111822	19159	0.1Mo	2.2s
norvégien	61844	0.6Mo	156548	57879	0.3Mo	2.9s

Figure 4 : Compression par epelle de plusieurs dictionnaires

---

---

fichier	nombre total de mots	mots différents	epelle	zpellout
dictionnaire français	239211	239211	71s	11s
/usr/dict/words	25144	25144	7s	1s
ce document	2488	754	1s	0.3s

Figure 5 : Temps de vérification de plusieurs fichiers

---

> writeto(`primes`);
> for i to 100000 do lprint(ithprime(i)) od:
> quit

% zpellin < primes > primes.z
% time zpellout primes.z < primes
1.97u 0.14s 0:02.11 100.0%

-rw-rw-r--   1 zimmerma eureca    341868 Jul 22 17:39 primes.z
-rw-rw-r--   1 zimmerma eureca    243061 Jul 22 17:39 primes.gz
-rw-rw-r--   1 zimmerma eureca    610196 Jun 28 18:02 words.french.gz
-rw-rw-r--   1 zimmerma eureca    505716 Jul 22 15:19 words.french.z

5  Implantation en C

5.1  Le fichier epelle.h

#include <stdio.h>
#include <ctype.h>

#define MAX_NODES 160000             /* maximal number of nodes after compaction */
#define PRIME 160001                /* must be greater than MAX_NODES */

#define I(a) ((unsigned int) a)

5.2  La fonction zpellin

/* Usage: zpellin < liste_mots > table */

#include "epelle.h"

#define C(a) ((char) a)
#define LOW(a) (a & 0xFF)
#define HIGH(a) ((a & 0xFF00)>>8)
#define VHIGH(a) ((a & 0x70000)>>16)
#define ERROR(s) {fprintf(stderr,"s\n"); exit(1);}

typedef struct NOEUD {
    char c,existe;
    struct NOEUD *fils,*frere;
} noeud;

noeud type_noeud[MAX_NODES];
int hashtab[PRIME];
int nb_noeuds=0,nb_types=0,traites=0;

noeud* nouveau_noeud(cc)
char cc;
{
    noeud *t;

    t = (noeud*) malloc(sizeof(noeud));
    if (t==0) ERROR(ran out of memory)
    t->c = cc;  t->existe = 0;  t->fils = t->frere = NULL; ++nb_noeuds;
    return(t);
}

main()
{
    noeud *root,*t;
    char cc;
    int nb_mots=0,i;

    t = root = nouveau_noeud('?');
    while ((cc = getchar()) != EOF)
        if ((unsigned)cc>' ')
          if (t->fils != NULL) {
           t = t->fils;
           while (t->c != cc)
               if (t->frere != NULL) t = t->frere;
               else t = t->frere = nouveau_noeud(cc);
          }
          else t = t->fils = nouveau_noeud(cc);
        else { t->existe = 1;  ++nb_mots;  t = root; }
    fprintf(stderr,"%d words, %d nodes, ",nb_mots,nb_noeuds);
    for (i=0;i<PRIME;i++) hashtab[i]=0;
    compactifie(root);
    fprintf(stderr,"%d nodes after compaction\n",nb_types);
    out();
    exit(0);
}

int hash (fi,fr,c,b)
int fi,fr;
char c,b;
{
    return(I(16061*fi + 16063*fr + 16067*I(c) + 16069*I(b)) % PRIME);
}

int cherche(fi,fr,c,b)
int fi,fr;
char c,b;
{
    int h,i;

    h = hash(fi,fr,c,b);
    while (hashtab[h] != 0) {
        i = hashtab[h];
        if (I(type_noeud[i].fils) == fi)
            if (I(type_noeud[i].frere) == fr)
                if (type_noeud[i].c == c)
                    if (type_noeud[i].existe == b)
                        return(i); /* trouve' */
        h = (h+1) % PRIME;
    }
    hashtab[h] = ++nb_types;
    return(-1); /* non trouve' */
}

int compactifie(t)
noeud *t;
{
    int type_frere, type_fils,i;

    if (t == NULL) return(0);
    else {
        traites++;
        type_frere = compactifie(t->frere);  type_fils = compactifie(t->fils);
        i = cherche(type_fils,type_frere,t->c,t->existe);
        if (i != -1) return(i);   /* sous-arbre de'ja` rencontre' */
        i = nb_types;
        if (i>=MAX_NODES) 
            {fprintf(stderr,"too many nodes : %d/%d\n",traites,nb_noeuds); exit(1);}
        type_noeud[i].c = t->c;  type_noeud[i].existe = t->existe;
        type_noeud[i].fils = (noeud*) type_fils;
        type_noeud[i].frere = (noeud*) type_frere;
        return(i);
    }
}

out() /* e'crit la table compacte'e en stdout   */
/* format : 6 octets par enregistrement         */
/*      0 : caracte`re                          */
/*      1 : boole'en + 3 bits + 3 bits vhigh    */
/*      2 : fils low                            */
/*      3 : fils high                           */
/*      4 : frere low                           */
/*      5 : frere high                          */
/* la racine est le dernier enregistrement      */
{
    int i,j,k;

    for (i=1; i<=nb_types; i++) {
        putchar(type_noeud[i].c);
        k = I(type_noeud[i].existe) + (VHIGH(I(type_noeud[i].fils))<<1)
            + (VHIGH(I(type_noeud[i].frere))<<4);
        putchar(C(k));
        putchar(C(LOW(I(type_noeud[i].fils))));
        putchar(C(HIGH(I(type_noeud[i].fils))));
        putchar(C(LOW(I(type_noeud[i].frere))));
        putchar(C(HIGH(I(type_noeud[i].frere))));
    }
}

5.3  La fonction zpellout

/* Usage: zpellout table < liste_mots > mots_errone's */

#include "epelle.h"

#define MAXLENGTH 256                   /* longueur maxi des mots */
#define CTOI(a) ((a<0) ? a+256 : a)

typedef struct NOEUD {
    char c,existe;
    unsigned int fils,frere;
} noeud;

noeud T[MAX_NODES];
int racine;

main(argc,argv)
int argc;
char* argv[];
{
    FILE *f,*fopen();
    char c,mot[MAXLENGTH],c1,c2;
    int i=0;

    /* entre'e de la table */
    f = fopen(argv[1],"r");
    while ((c = getc(f)) != EOF) {
        T[++i].c = c;
        c =  getc(f);
        T[i].existe = I(c) & 0x1;
        c1 = getc(f); c2 = getc(f);
        T[i].fils = CTOI(c1) + (CTOI(c2) << 8);
        c1 = getc(f); c2 = getc(f);
        T[i].frere = CTOI(c1) + (CTOI(c2) << 8);
        T[i].fils += (I(c) & 0xE) << 15;
        T[i].frere += (I(c) & 0x70) << 12;
    }
    racine = i;
    /* boucle de de'tection de mots errone's */
    i = 0;
    while ((c = getchar()) != EOF)
        if ((unsigned)c>' ') mot[i++] = c;
        else { 
            mot[i] = 0; 
            /* un mot est accepte' lorsqu'en mettant toutes ses lettres
               en minuscules, on trouve un mot du dictionnaire */
            if (!valide(mot)) printf("%s\n",mot);
            i = 0;
            }
    exit(0);
}

int valide(s)
char *s;
{
    int i,t; 
    char c;

    i=0; t=racine;
    while ((c = tolower(s[i])) != 0) {
        if (T[t].fils == 0) return(0); /* non valide */
        t = T[t].fils;
        while (T[t].c != c)
            if (T[t].frere == 0) return(0); 
     else t = T[t].frere;
        i++;
    }
    return(I(T[t].existe)); /* 0 ou 1 */
}

Remerciements.

Ce document a été traduit de L^AT_EX par H^EV^EA.