Problem:
Input: The line L is given as input in the form of two end points. The input for triangle T is given in the form of three points (its three vertices v0, v1 and v2).
Output: We return the type of intersection (see the list below) and the vertices or the edges involved.

                    proper intersection
                    no intersection
                    intersection at a vertex
                    intersection on an edge
                    coplanar and no intersection
                    coplanar and intersection at vertex
                    intersection through two edges
                    intersection contains an edge
                    intersection through one vertex and an edge

Robustness issues

Representation:
We use the plucker coordinates to solve this problem. We compute the side-operator of the line  L with the three oriented lines e1(v0 to v1), e2(v1 to v2) and  e3(v2 to v0) supporting the edges of the triangle.

S1 = side-operator(L,e1)
S2 = side-operator(L,e2)
S3 = side-operator(L,e3)
 

Different possible cases:
1) The triangle and the lines are not coplanar

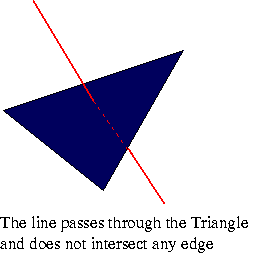
proper intersection S1, S2, S3 <0  Or S1, S2, S3 >0

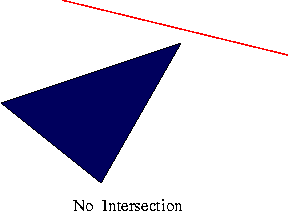no intersection S1, S2 and S3 don't all have the same sign

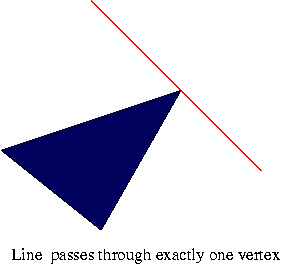intersection at a vertex Two out of S1, S2, S3 are equal to zero

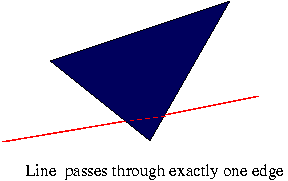Intersection on an edge One of the three S1,S2,S3 is zero and the other two have same sign (>0 or <0)

2) The triangle and the lines are coplanar, then  S1 = S2 = S3 = 0 Let p be a point not coplanar with the triangle T. Let T1, T2 and T3 denote the triangle (v0,v1,p), (v1,v2,p) and (v2,v0,p). Notice that the line and the triangle Ti are not coplanar.The following cases are solved by intersecting the line L and the triangles Ti , as in case 1

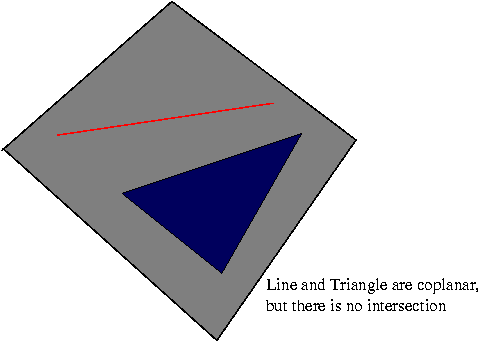Coplanar and no intersection Intersection of L and Ti returns "no intersection" for all i = 1,2,3.

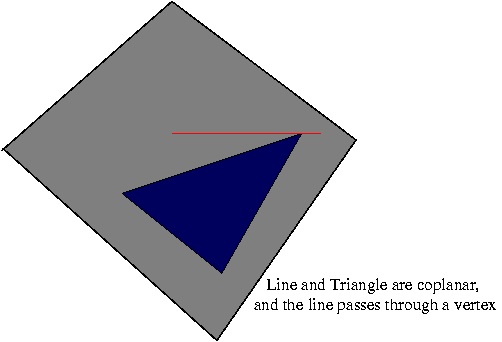Coplanar and intersection at a vertex Intersection of L and one of the Ti returns "no intersection" and intersection of L and the other two Ti returns "intersection at a vertex"

Intersection through two edges Intersection of L and two of the Ti returns  "intersection on an edge" and the intersection with the remaining Ti returns "no intersection"

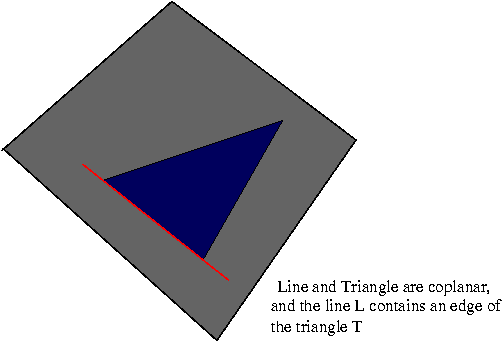Intersection contains an edge Intersection of L and two of Ti returns "intersection at a vertex" and the intersection of L and the remaining Ti will result in the line and the triangle being coplanar

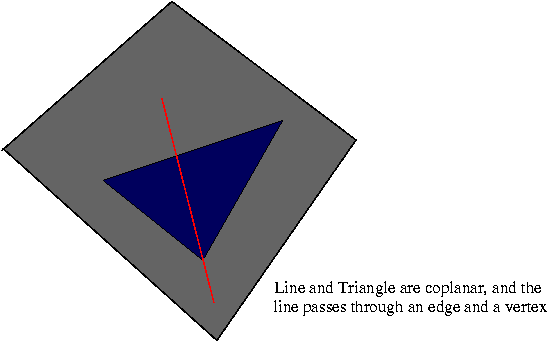Intersection through one vertex and an edge Intersection of L and two of the Ti will return "intersection at a vertex" and the intersection with the remaining Ti returns "intersection on an edge"

Code:
The code can be found here.

Prepared by Anoop Pant (anoop.pant@mailcity.com)
Contact : hazel.everett@loria.fr, sylvain.lazard@loria.fr,sylvain.petitjea@loria.fr

Last modified : 18/8/2001