Connected components of line segment transversals
Report on progress at the 2003 Bellairs GIG
Coordinator: Frank Sottile

---

Problem #3: Determine the number of connected components of the set of common transversals to 4 line segments.
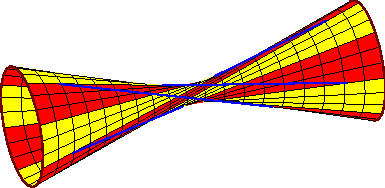
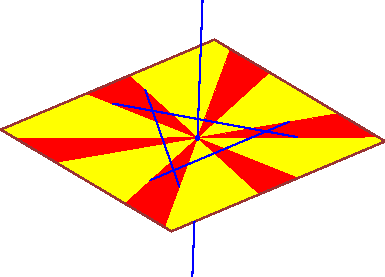
Progress: The question makes sense for any number n of line segments. The bound is 2 except in 3 special degenerate cases. Assuming that n is at least 4, we show that the maximum number of components is n, and this occurs only if the segments all lie along the lines in one ruling of a hyperboloid of one sheet. (All smaller numbers can occur, as well). For n>4, there can also be up to n connected components if all segments are coplanar. 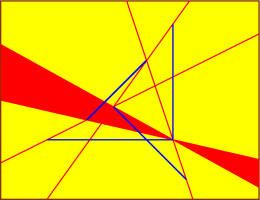(This is n-1 if there are n-1 coplanar segments and one non-coplanar segment.) Finally, in addition to these cases, when n=4, there can be three connected components if the segments intersect pairwise. 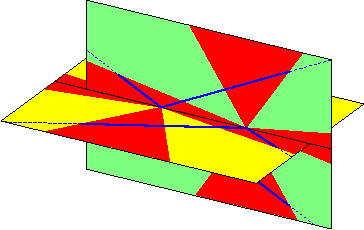Pictures of all these extreme geometries are presented below. In these pictures, the lines segments are blue and the common transversals are in red. As there are infinitely many common transversals, they form red regions on the axillary surfaces that we also draw.
       
        Plan: There is a short manuscript detailing (mostly) the proof. It needs to be fleshed out, revised, and then rewritten to conform to the standards and style of the journal to which we will submit it.