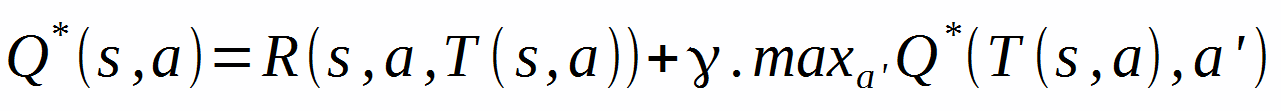|
|
 Page web Vincent THOMAS
Atelier ISN - 30/03/2017
"Construction de comportements intelligents"
Plan de la page
- Contenu Principal - Atelier 2017
- Complément - Atelier 2016
L'ensemble des fichiers de cette page sont disponibles en version compressée à partir de ce lien
Description de l'atelier
La planification d'actions consiste pour un agent informatique (par ex, un robot) à construire le comportement à suivre pour réaliser un objectif (atteindre un lieu, transporter un objet, ...). C'est un problème difficile car il faut raisonner sur le long terme et prendre en compte de nombreux facteurs (ressources disponibles, ...).
L'atelier aura pour objectif de présenter et mettre en oeuvre (en python) un algorithme générique nommé 'value iteration' permettant à un agent de planifier ses actions sur le long terme. Cet algorithme, basé sur la programmation dynamique, est simple à implémenter, adapté à de nombreux problèmes et facilement utilisable dans des projets d'intelligence artificielle.
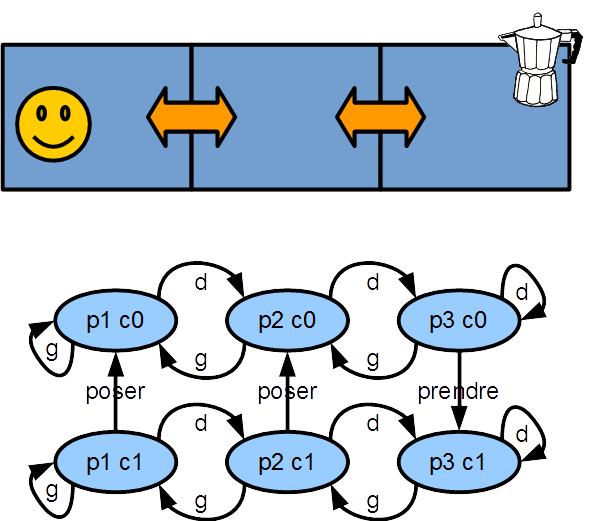
- (1) Dans un premier temps, on proposera un moyen de représenter (et de coder) simplement un problème de prise de décision (sous la forme d'un automate représenté de manière compact - cf figure).
- (2) Dans un second temps, on s’intéressera à l'équation de Bellman qui exprime le lien entre les actions entreprises et leurs conséquences sur le long terme.
- (3) Enfin, à partir de l'équation de Bellman, on mettra en œuvre l'algorithme d’itération sur la valeur qui permet de construire un comportement capable de résoudre optimalement le problème donné.
On illustrera cette approche en traitant des problèmes très simples mais qui nécessitent de construire des comportements intelligents (transport d'objets, labyrinthe avec portes et clefs).
Outils à installer
Dans cet atelier, le langage utilisé sera python 3.
Afin de pouvoir afficher le comportement appris, on affichera différentes animations. On utilisera pour cela la bibliothèque "pygame" (cf atelier sur la création de jeux et d'animation). Le code permettant de gérer l'affichage sera fourni pendant l'atelier.
Pour pouvoir aborder cet atelier, si vous souhaitez utiliser votre machine, on vous propose d'installer la distribution
EduPython (disponible à l'adresse http://edupython.tuxfamily.org/)
qui inclut nativement la bibliothèque pygame.
Si vous avez des idées de problèmes de décision ou de contrôle qui vous intéressent, nous pourrons en discuter ou le résoudre lors de l'atelier (vous pouvez aussi m'envoyer un mail au préalable - vincent.thomas@loria.fr)
Documents 2017
L'atelier 2017 s'est structuré autour des documents suivants
Les fichiers contenus dans le fichier zip ci-dessus correspondent à des contenus différents
Résumé de l'atelier
Modélisation d'un problème de décision
Dans un premier temps, l'atelier cherche à modéliser les problèmes de prise de décision dans un cadre simple que sont les "processus de décision markoviens" déterministe (MDP déterministe).
Ce cadre formel se représente en quelques méthodes.
- méthode actions(self)
=> retourne la liste des actions possibles ;
- méthode etats(self)
=> retourne la liste des états accessibles ;
- méthode transition(self,s,a)
=> retourne l'état d'arrivée lorsqu'on part de s et qu'on fait l'action a ;
- méthode recompense(self,s,a,sarr)
=> retourne la récompense immédiate lorsqu'on part de s et qu'on fait l'action a et qu'on arrive en sarr.
Le cadre général est fourni dans le fichier  00_cafe_probleme_vide et correspond au code ci dessous.
class Cafe:
""""permet de definir un probleme"""
def actions(self):
"""retourne la liste d'actions"""
return([])
def etats(self):
"""retourne la liste d'etats"""
return([])
def transition(self,s,a):
"""definit les consequence d une action"""
return(s)
def recompense(self,s,a,sarr):
"""definit la recompense obtenue"""
return(0)
Le second fichier 02_cafe_intelligent_vide contient la modélisation du problème du café (cf slides).
class Cafe:
def actions(self):
""" definit l'ensemble d'actions possibles """
return(['gauche','droite','prendre','poser'])
def etats(self):
""" definit l'ensemble d'etats possibles """
return([(1,0),(1,1),(2,0),(2,1),(3,0),(3,1)])
def transition(self,s,a):
""" definit les consequences d'une action """
pos=s[0];
cafe=s[1];
if (a=='gauche'):
if (pos>1):
pos=pos-1
if (a=='droite'):
if (pos<3):
pos=pos+1
if (a=='prendre'):
if (pos==3):
cafe=1
if (a=='poser'):
cafe=0
return(pos,cafe);
def recompense(self,s,a,sarr):
""" definit les recompenses obtenues """
if (s[0]==1) and (s[1]==1) and (a=='poser'):
return(100)
return(-1)
Équation de Bellman
Une fois le problème défini, on s'attardera à la propriété mathématique que la solution (comportement optimal de l'agent) doit vérifier.
Cette propriété s'exprime sur les Q-valeurs représentant l'espérance de gain maximale qu'il est possible d'obtenir quand on part de l'état s et que l'on fait l'action a.
Cette propriété est définie par l'équation d'optimalité de Bellman qui fait le lien entre ce que l'on peut espérer gagner à l'instant t et ce que l'on peut espérer gagner à l'instant t+1. Ce lien s'exprime simplement de la manière suivante :
--- Ce que l'on peut gagner au mieux en partant de s et en faisant l'action a est égal à la récompense immédiate obtenue additionnée à ce qu'on pourra obtenir en choisissant la meilleur action dans l'état d'arrivée ---
Cette équation s'exprime ainsi de la manière suivante pour tout s et tout a :
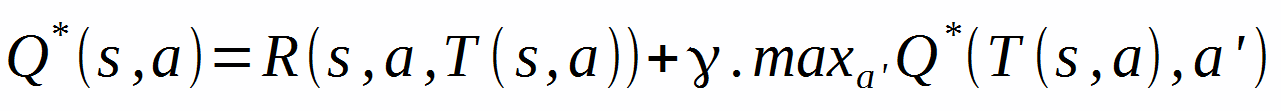
Algorithme d'itération sur la valeur
On étudiera un algorithme basé l'application itérée de l'équation d'optimalité de Bellman. Cet algorithme nommé "iteration sur la valeur" permettra de résoudre les problèmes de décision présentés ci-dessus.
L'algorithme consiste simplement à appliquer à chaque pas de temps l'équation de Bellman ci-dessus. Cette suite récurrente converge vers un ensemble de Q-valeurs qui vérifient la propriété d'égalité (théorème du point fixe - cf transparents pour plus d'informations).
L'algorithme d'iteration sur la valeur peut donc s'écrire comme dans le fichier 03_cafe_intelligent_complet
- valueIteration(self,nb)
=> exécute value iteration pendant nb iterations.
- executerUneIteration(self,Q,gamma)
=> execute une iteration de value iteration. La méthode part d'une Q valeur à t et retourne Q à t+1 en applicant l'équation de bellman.
- chercherMax(self,Q,sArriv)
=> cherche simplement la meilleure action dans l'état s selon les Qvaleurs calculées. Cette méthode est juste en charge du max dans l'équation de bellman.
def valueIteration(self,nb):
"""effectue algorithme value iteration"""
gamma=0.99
# initialiser les Q valeurs
Q=self.intialiseQ()
# faire nb iteration
for i in range(0,nb):
# creer une mise a jour de Qvaleurs
Q = self.executerUneIteration(Q,gamma)
#affiche Q
print('*** iteration '+str(i)+' ****')
self.afficherQ(Q)
# retourne Qvaleurs
return(Q)
def executerUneIteration(self,Q,gamma):
""" effectue une iteration de value iteration """
#initialiser Q2
Q2={}
#pour chaque etat
for etat in self.pb.etats():
#pour chaque action
for action in self.pb.actions():
# calculer arrivee et recompense
sArriv=self.pb.transition(etat,action)
r=self.pb.recompense(etat,action,sArriv)
# cherche max arrivee (utiliser chercherMax)
max=self.chercherMax(Q,sArriv)
#mise a jour de Q2
Q2[(etat,action)]=r+gamma*max
#retourne Q2
return(Q2)
def chercherMax(self,Q,sArriv):
""" cherche la valeur maximale sur un etat"""
max=-100000;
#pour chaque action
for actionMax in self.pb.actions():
#si la clef n'existe pas, on cree
if (not((sArriv,actionMax) in Q)):
Q[(sArriv,actionMax)]=0
#si la valeur est plus grande que max, c'est le max
if (Q[(sArriv,actionMax)]>max):
max=Q[(sArriv,actionMax)]
#retourne max
return(max)
Algorithme Q-learning
Il est possible d'étendre le contenu de l'atelier de 2017 dans plusieurs directions
- en introduisant de l'aléatoire dans les résultats des actions (on utilise alors le cadre formel générique des MDP et l'équation de Bellman est légèrement modifiée pour intégrer une espérance)
- en proposant d'aborder le problème d'apprentissage par renforcement dans lequel un agent ne connait pas le monde mais va essayer d'apprendre comment agir en y testant des actions.
Ces différents éléments ont été abordés dans l'atelier 2016 dont les documents sont reproduits ci-dessous.
En particulier, à partir d'une variation de l'algorithme Value iteration, l'atelier 2016 a cherché à présenter l'algorithme du "Q-learning" qui permet à un agent de modifier progressivement son comportement en fonction de ses expériences afin de résoudre un problème donné.
Contenu de atelier 2016
L'atelier 2016 était plus complexe que celui présenté en 2017. Il souhaitait aborder
- la définition d'un probleme (cf 2017)
- l'équation de bellman avec de l'aléatoire (cf 2017)
- l'algorithme value iteration (cf 2017)
- l'algorithme QLearning (nouveauté par rapport à 2017)
Les transparents sont accessibles à partir de ce lien:  Slides_ISN2016_ApprentissageRenforcement.
Les différents éléments de issus 2016 sont organisés de la manière suivantes:
Problèmes abordés 2016
Une fois qu'on aura établi un cadre permettant de représenter des problèmes de décisions, on travaillera sur différents types de problèmes possibles.
Pour montrer l'aspect générique de l'approche, ces problèmes sera abordés avec la même formalisation et résolu avec les mêmes algorithmes. L'ensemble des fichiers sources seront disponibles à la fin de l'atelier.
Enfin, il est à noter que ces problèmes se placent parfois dans le cadre général de problèmes stochastique (avec du hasard). Ainsi, pour les problèmes (c) et (d), le résultat de la fonction de transition n'est pas un simple état mais une distribution de probabilité sur les états atteignables.
Par exemple [(s1,0.7),(s2,0.2),(s3,0.1)] signifie
- qu'on a une probabilité de 0.7 d'arriver en s1
- qu'on a une probabilité de 0.2 d'arriver en s2
- qu'on a une probabilité de 0.1 d'arriver en s3
La somme des probabilités est bien égale à 1 (contrainte nécesaire pour avoir une distribution de probabilité correcte).
a) Recherche de chemin dans un labyrinthe
L'agent doit parcourir un labyrinthe pour atteindre son objectif le plus rapidement possible tout en évitant des obstacles.
Lorsque l'agent traverse un obstacle, il reçoit une récompense négative de -20. A chaque déplacement, il reçoit une récompense négative de -1. Enfin, lorsqu'il atteint l'objectif, il reçoit une récompense de +100.
Probleme Labyrinthe
|
|
 |
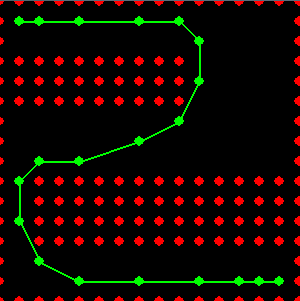
b) Course sur petits carreaux "RaceTracker"
Dans ce jeu, l'objectif est de contrôler une voiture de course dont la dynamique (vitesse et accélération) est modélisée de manière très simple: à chaque pas de temps, la voiture se déplace sur une nouvelle case correspondant au symétrique de son ancienne case par rapport à sa position actuelle. Le joueur peut accélérer ou décélérer en choisissant une case adjacente à la case d'arrivée initiale.
Ainsi, quand un déplacement est important, le déplacement aura aussi tendance à l'être (ce que simule la symétrie). Il faut donc du temps pour accélérer ou décélérer.
Probleme RaceTracker
Liens sur le jeu:
|
|
 |
c) Orientation + probabilité de glisser
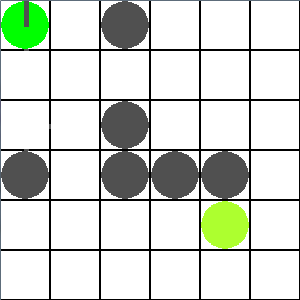
Dans ce problème, un agent doit atteindre un but (représenté par le cercle vert). Il est caractérisé par une position et une orientation et peut à chaque instant soit changer son orientation d'un quart de tour, soit avancer devant lui.
Lorsque l'agent avance, il a une chance sur deux d'avancer de deux cases au lieu de une.
Lorsque l'agent tombe dans un trou, il reçoit une récompense négative et ne peut plus en sortir
Problème orientation et probabilité de glisser
|
|
|
d) Maintien de niveaux dans des clepsydres.
Dans ce problème, un agent doit se déplacer dans un environnement pour maintenir le niveau d'eau dans différentes clepsydre. Le problème est compliqué car remplir les clepsydre nécessite de se déplacer dans l'espace, car les clepsydres ont différents niveaux de remplissage possibles (ce qui se traduit par des récompenses différentes), à chaque pas de temps, il y a une certain probabilité qu'une clepsydre se vide d'un niveau.
Probleme clepsydre + affichage graphique (pygame)
|
|
|
Fichiers utiles
Ces fichiers présentent les différents problèmes et leurs solutions. A noter qu'il est nécessaire dans certain cas de disposer de la bibliothèque pygame pour pouvoir afficher un rendu graphique.
La section sur les outils présente comment l'installer.
- Problèmes
- Execution
- Value Iteration
- Apprentissage par renforcement
- Problèmes stochastiques
- Solution complètes
- Lampe
- Labyrinthe
- ChercheurOr (simple)
- RaceTracker
- Orientation et probabilité de glisser
Références
- Liens wikipedia pour approfondir ce qui sera présenté dans l'atelier :
- Sur le conditionnement opérant
- Sur les problèmes de décision
Icons  designed by {Freepik} from Flaticon.
|
|
|