- Preliminaries
- RSA, and integer factorization problem
- Diffie-Hellman, and the discrete logarithm problem
- Pairings
- How to stay up-to-date (veille technologique)
- Index, English-French
These lecture notes are about integer factorization, discrete logarithm computation, and pairings on elliptic curves, all for asymmetric cryptography.
Preliminaries
Introduction: public-key cryptography
Public-key cryptography, or asymmetric cryptography, is quite recent, it was introduced in 1976 and 1977 with two cryptosystems, RSA (Rivest, Shamir, Adleman) and DH (Diffie-Hellman). In a public-key system, the keys are asymmetric, in the sense that the encryption key and the decryption key are different, and it is a very hard mathematical problem to find the decryption key while knowing only the public key (and the public parameters). It is an active research area to challenge believed hard mathematical problems used in cryptography, and looking for new hard problems. Nowadays two hard mathematical problems are at the heart of public-key (or asymmetric) cryptography: hardness of integer factorization with the RSA cryptosystem, and discrete logarithm computation, related to the hardness of the Diffie–Hellman problem.
Textbooks
Christof Paar and Jan Pelzl. Understanding Cryptography, a Textbook for Students and Practitioners. Springer, 2010. DOI 10.1007/978-3-642-04101-3
(Two textbooks are available at the library at Lorient, code 005.8 PAA).
During lockdown, the library is opened: see La BU sur rendez-vous
Pendant le confinement, la BU reste ouverte sur RDV : voir La BU sur rendez-vous
Relvant chapters: 6, 7, 8 and 10.
- Schnorr signature, patented until February 2008, on Wikipedia
- Digital Signature Algorithm (DSA), textbook (Paar Pelzl) Chapter 10 section 4 page 277, Handbook of Applied Cryptography Chapter 11 section 5.1 (11.5.1), on Wikipedia, NIST FIPS 186-4 Section 4
- ECDSA (elliptic curve DSA), textbook (Paar Pelzl) chapter 10 section 5 (10.5 page 282), NIST FIPS 186-4 Section 6
On the webpage of Pr. Alfred Menezes one finds the chapters of the Handbook of applied cryptography, the relevant chapters are chapter 3, section 3.3 on the RSA problem, section 3.6 on the discrete logarithm problem, section 3.7 on the Diffie-Hellman problem; chapter 8, section 8.2 on public-key cryptography and RSA, section 8.4 on ElGamal encryption, and Chapter 11, section 5.2 (11.5.2) on ElGamal signature scheme, section 5.1 (11.5.1) on Digital Signature Algorithm.
In the following notes, the original research papers are given (name of authors, title of paper, journal or conference where the results were published). In many cases, only the abstract of the paper is available on the editor’s website, the PDF of the paper it accessible only after a paywall, or through identification (you can try through eduroam, or try institutional identification, then try (Log in via Shibboleth or Athens). Alternatively, a seach on public archives can sometimes provide a free version:
You don’t need to read these papers for the course.
RSA, and integer factorization problem
Textbook Understanding cryptography, Chapters 6 and 7.
Handbook of applied cryptography, section 3.3 of Chapter 3 and section 8.2 of Chapter 8.
Wikipedia: RSA cryptosystem, available in many languages (links on the left of the page).
In French: https://members.loria.fr/AGuillevic/files/teaching/NFS/techniques-de-l-ingenieur-record-calcul-RSA240.pdf
Introduction on RSA
RSA, how does it work?
In 1977, Ron Rivest, Adi Shamir, and Leonard Adleman design an asymmetric encryption scheme. It requires a modulus N, it is an integer, the result of a multiplication of two distinct prime numbers p and q. Arithmetic operations are performed modulo N: addition, subtraction, multiplication and inversion. But other operations are hard (take an extremely long time) if nothing more than N is known: computing a square root: sqrt(x) = x1/2 modulo N is hard, computing x1/n modulo N is hard, because the order of the multiplicative group is not known.
The multiplicative group is the set of elements x in {1, 2, 3, …, N-1} that have an inverse 1/x modulo N. To be invertible, x needs to be co-prime to N, that is, x and N have no common factor. But since N = p · q and p, q are prime, one can list the numbers that are not coprime to N: they are {p, 2p, 3p, …, (q-1)p} (set of q-1 numbers) and {q, 2q, 3q, …, (p-1)q} (set of p-1 numbers). Removing (q-1+p-1) integers from the set {1, 2, …, N-1}, there are N-1-(q+p-2) = pq –p–q+1 = (p-1)(q-1) integers in the multiplicative group. But computing the value (p-1)(q-1) without knowing p and q is very hard when N is large enough (more than 600 decimal digits for example).
The encryption scheme of Rivest, Shamir and Adleman works as follows, between two parties usually named Alice and Bob.
- Alice chooses two distinct primes p and q and computes N= pq. She chooses a positive integer e coprime to p and q (in reference standards, e = 216 + 1 = 65537) and she computes d the inverse of e modulo (p – 1)(q – 1), so that ed = 1 mod (p – 1)(q – 1). Her public key is the pair (N, e) and her secret key is made of the three numbers (p, q, d);
- Bob reads Alice’s public key (N, e); he encodes his secret as a number m between 1 and N – 1. To encrypt m, he computes c = me mod N and sends c to Alice;
- Alice receives c and computes cd mod N. She has cd = med = m mod N.
The public exponent e is for encryption, and the private exponent d is for decryption. It works because with ed = 1 mod (p – 1)(q – 1), one has med = m mod N. The security of this scheme relies on the hardness of computing the secret exponent d, knowing only N and the public exponent e. The secret number p and q are required to compute d, hence the security of RSA relies on the hardness of factoring N.
In practice, one can generate a pair of asymmetric keys with ssh-keygen in a Linux shell, with PGP for emails (Enigmails on Thunderbird, Protonmail for example).
Note that short keys are not allowed:
ssh-keygen -b 512 -t rsa -f key_example_512
Invalid RSA key length: minimum is 1024 bitsssh-keygen -b 1024 -t rsa -f key_exampleThe files key_example (with the private key) and key_example.pub (public key, public exponent) are encoded in Base64.
Knowing the public and private exponents gives a factorization of N
Knowing d and e satisfying ed = 1 mod (p-1)(q-1), one can factor N and recover p and q.
For all x in {1, …, N-1} coprime to N, we have xed-1 = 1 mod N because ed-1 = 0 mod (p-1)(q-1), and x(p-1)(q-1) = 1 mod N. Since p and q are prime, (p-1)(q-1) is even (it is a multiple of 4) and since ed-1 is a multiple of (p-1)(q-1), it is a multiple of 4. We can divide ed-1 by two: (ed-1)/2 is an integer.
We compute y = x(ed-1)/2. It is a square root of 1. If the result y is not 1 or -1, then we have y2 = 12 mod N, that is y2 – 12 = (y-1)(y+1) = 0 mod N. Hence y-1 and y+1 share a factor with N. We compute gcd(y-1, N) to find a factor p or q.
If the value of y is 1 or -1, then we can do the same but with y = x(ed-1)/4, y = x(ed-1)/8, and divide the exponent by increasing powers of 2 as long as the result is an integer. If it fails, we can try with another x. In practice, the chances of success are very high (only a few x are needed).
Short private exponent is a bad idea
Wiener found an attack when the private exponent d is very small compared to N.
Padding
With a modulus N, one can encrypt messages m between 0 and N – 1. But if m is 0, 1 or much smaller than N, it produces a bias, and problems can happen. For example, the ciphertext of 0 is 0 (if m = 0, me = 0 mod N), the ciphertext of 1 is 1 (if m = 1, me = 1 mod N), and if m is between 2 and N1/e (the nearest integer to the e-th root of N), there is no modular reduction, c = me as integers. RSA encryption scheme cannot be used directly as described above. It should be used with a good padding, that is a way to fill the unused bytes of data when m is shorter (in bytes) than N.
In particular, if a symmetric key of 128 bits (16 bytes) is encrypted with a 2048-bit modulus N (256 bytes), then 2048 – 128 = 1920 bits (240 bytes) are free. Standards like PKCS describe secure ways of implementing a padding (filling the zeros).
Choosing key sizes
Contrary to symmetric cryptography where the key sizes are usually 128, 192 or 256 bits, with RSA the key sizes are much larger. Cryptographers are interested in comparing the security of asymmetric cryptosystems to the security of symmetric ciphers (like AES). For a perfect symmetric cipher, whose secret key has length n bits, the generic attack consists in testing all the 2n possible keys. This is also called brute-force search. Hence a symmetric cipher of keylength n bits is said to provide n bits of security. The length of RSA modulus N is designed in order to ensure that an attacker attempting to factor N would need as much time as for breaking a perfect symmetric encryption with a key of 128, 192, or 256 bits. Because the hardness of factoring grows slower, the key sizes are much larger.
In a web browser, one can check the cipher suite used for securely connecting to a https website. A cipher suite is made of a public-key and a private-key encryption system.
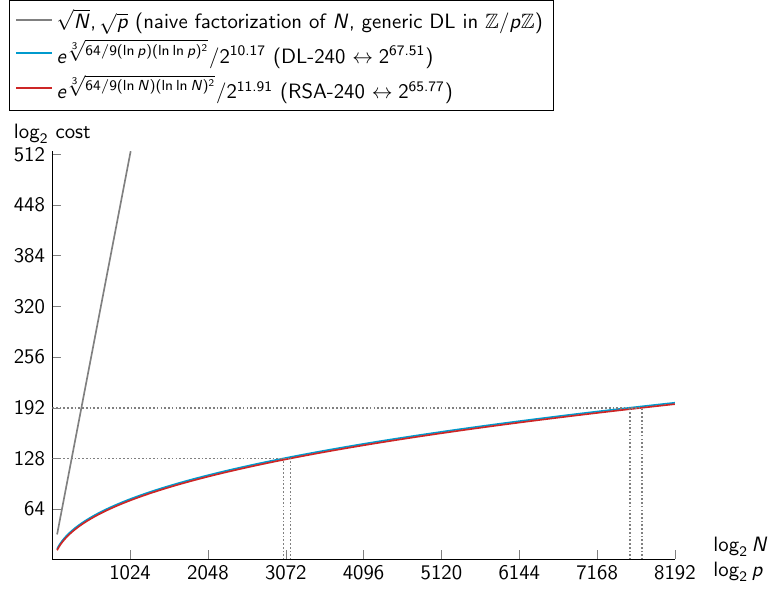
Graph of complexity of integer factorization, discrete logarithm with NFS, and generic DL computation
Particles
| n | 2n | Examples |
|---|---|---|
| 32 | 232 = 109.6 | number of humans on Earth |
| 46 | 246 = 1013.8 | distance Earth – Sun in millimeters, number of operations in one day on a processor at 1 GHz |
| 55 | 255 = 1016.6 | number of operations in one year on a processor at 1 GHz |
| 82 | 282 = 1024.7 | mass of Earth in kilograms |
| 90 | 290 = 1027.1 | numer of operations in 15 billion years (age of the universe) on a processor at 1 GHz |
| 155 | 2155 = 1046.7 | number of molecules of water on Earth |
| 256 | 2256 = 1077.1 | number of electrons in universe |
(Courtesy Marine Minier)
Boiling water
Lenstra, A.K., Kleinjung, T., Thomé, E.: Universal Security; From bits and mips to pools, lakes – and beyond. In: Fischlin, M., Katzenbeisser, S. (eds.) Number Theory and Cryptography. LNCS, vol. 8260, pp. 121-124. Springer, Darmstadt, Germany (Nov 2013). DOI 10.1007/978-3-642-42001-6_9, HAL 00925622.
- 290 operations require enough energy to boil the lake of Genève
- 2114 operations: boiling all the water on Earth
- 2128 operations: boiling 16000 planets like the Earth
Attacking RSA with Integer Factorization
One way of breaking RSA encryption is to factor the modulus N into p times q. Then, computing d = 1/e mod (p – 1)(q – 1) is easily done with an extended gcd algorithm (with SageMath for example).
Naive way 1: Testing all primes up to square root of N
For very small numbers (up to 1000 for example), factoring it can be done by trying to divide it by all the prime numbers up to its square root. In math software this is called trial division. For large numbers this is impracticable: there are too many possible prime factors. There are about N/ln N prime numbers up to N, where ln is the logarithm in basis e (not in basis 10). Restricting the search to the prime numbers up to the square root of N, it still has a cost of roughly the square root of N over log N tests.
| N (bits) | N (digits) | sqrt(N)/ln(sqrt(N)) |
|---|---|---|
| 256 | 77 | 2122, 1037 |
| 512 | 154 | 2249, 1075 |
| 768 | 231 | 2376, 10114 |
| 1024 | 308 | 2504, 10152 |
| 1280 | 385 | 2632, 10191 |
| 1536 | 462 | 2759, 10229 |
| 1792 | 539 | 2887, 10267 |
| 2048 | 617 | 21015, 10306 |
| 2304 | 694 | 21143, 10344 |
| 2560 | 771 | 21271, 10383 |
| 2816 | 848 | 21399, 10421 |
| 3072 | 925 | 21526, 10460 |
from math import log as ln
from math import ceil
for log2N in range(256, 3072+1, 256):
log10N = int(round(log2N*ln(2)/ln(10)))
s2 = int(ceil(log2N/2 - ln(log2N/2*ln(2))/(ln(2))))
s10 = int(ceil(log2N/2 * ln(2)/ln(10) - ln(log2N/2 * ln(2))/ln(10)))
print("| {:4d} | {:4d} | 2^{:d} | 10^{:d} |".format(log2N, log10N, s2, s10))This technique is completely impracticable even for numbers of 30 digits, because there are too many prime numbers that need to be tested.
Naive way 2: testing all primes around square root of N
Actually we know that p and q are both of the same size. How many primes are they between 2n-1 and 2n where n is the expected size of p and q?
count = 2n/ln(2n) – 2n-1/ln(2n-1) = 2n-1(2/(n ln 2) – 1/((n – 1) ln 2)) = (2n-1/ln 2) · (2/n – 1/(n – 1)) approximately (1/2) · (2n / ln 2n)
from math import log as ln
from math import ceil
for log2N in range(256, 3072+1, 256):
log10N = int(round(log2N*ln(2)/ln(10)))
n = log2N / 2
c = (n-1)*ln(2) + ln((n-2)/(ln(2)*n*(n-1)))
c2 = int(ceil(c/ln(2)))
c10 = int(ceil(c/ln(10)))
print("| {:4d} | {:4d} | 2^{:d} | 10^{:d} |".format(log2N, log10N, c2, c10))| N (bits) | N (digits) | count: prime numbers around sqrt(N) |
|---|---|---|
| 256 | 77 | 2121, 1037 |
| 512 | 154 | 2248, 1075 |
| 768 | 231 | 2375, 10113 |
| 1024 | 308 | 2503, 10152 |
| 1280 | 385 | 2631, 10190 |
| 1536 | 462 | 2758, 10229 |
| 1792 | 539 | 2886, 10267 |
| 2048 | 617 | 21014, 10306 |
| 2304 | 694 | 21142, 10344 |
| 2560 | 771 | 21270, 10383 |
| 2816 | 848 | 21398, 10421 |
| 3072 | 925 | 21525, 10460 |
There are again many prime numbers of a fixed size in bits. It is only two times faster than the previous method (for example the first rows of both tables say 2122 = 2 × 2121). It is not feasible.
Historical steps in integer factorization
- 1975, Morrison, Brillhard, continued fraction method CFRAC, factorization of the 7-th Fermat number 227+1 = 2128+1 (see the Cunningham project)
2128+1 = 340282366920938463463374607431768211457 = 59649589127497217 × 5704689200685129054721 - 1981, Dixon, random squares method
- 70’s, unpublished: Schroeppel, Linear Sieve
- 1982, Pomerance, Quadratic Sieve
- 1987, Lenstra, Elliptic Curve Method (ECM)
- 1993, Buhler, Lenstra, Pomerance, General Number Field Sieve
A strong joint work between academia and industry in particular in the US: showing that very large computations can be run on computers was a selling argument for industrial too (it was before the personal computer).
Quadratic sieve
Find a very different approach: we know that N is the product of two prime numbers.
Square roots modulo N
In a field like the real numbers R, a positive number n has two square roots: +sqrt(n) and -sqrt(n). But in a ring of integers modulo N =pq, strange things happen: if a number is a square, it has four square roots.
Example: N = 2021 = 43 × 47
12 = 1 mod 2021
(-1)2 = 1 mod 2021
9882 = 1 mod 2021
(-988)2 = 1 mod 2021
N = 2021
for i in range(-N//2, N//2):
if (i**2 % N) == 1:
print(i)We have two pairs of square roots of n=1: (1, -1) and (988, -988). Then, observe that
9882 = 12 mod 2021
⇔ 9882 – 12 = 0 mod 2021
⇔ (988 – 1) · (988 + 1) = 0 mod 2021
Compute a gcd: gcd(988 – 1, N) = 47, hence 47 divides N. Indeed N = 43×47. (It works with gcd(988 + 1, N) = 43 too.)
Aim of the quadratic sieve method: finding a relation X2 = Y2 mod N, where X is different from Y and –Y, to obtain a factorization (X – Y) · (X + Y) which is a multiple of N. Then finding the factorization of N by computing a gcd of N with X – Y or X + Y.
But of course, we cannot enumerate the squares of numbers modulo N to find a match, and none of the methods for computing a square root in a field will work.
Brilliant idea: enumerate smoothness relations, then combine them to obtain a combination of squares.
Numerical example
Again one starts with N = 2021. One would like to find an equality modulo N with a distinct square on both sides. Start with a square on the left-hand side, and factor the right-hand side (as an integer) into a product of small primes. Hope to be able to combine the relations to obtain a square on the right too.
One starts with enumerating the integers right above sqrt(N). Their square is larger than N, hence the operation modulo N subtracts N. In other words, set m = round(sqrt(N)) the nearest integer to the square root of N, and lists all small integers a such that
the integer (m+a)2 – N is the product of small primes only.
m = 45 (where sqrt(2021) = 44.955…)
(1+m)2 – N = 95 = 5 × 19
(4+m)2 – N = 380 = 22 × 5 × 19
(16+m)2 – N = 1700 = 22 × 52 × 17
→ We enumerated the a from 1 to 20.
The left-hand side of the relations is a square by design, let us concentrate on the right-hand side. One combines the first and second relation: multiplying the two left-sides, and separately the two right-sides: one obtain that
(1+m)2 · (4+m)2 = 22 · 52 · 192 mod N ⟹ (46 · 49)2 = (2 · 5 · 19)2 mod N
Set X = 46 · 49 = 2254 = 233 mod N, Y = 2 · 5 · 19 = 190, and finally gcd(233 – 190, N) = 43, we found a factor of N. It works with gcd(233 + 190, N) = 47, this is the other factor of N.
This method keeps only the relations modulo N with small primes for two reasons:
- easier to factor a number if we know that is has only small factors. If no small factor is found, the factorization process is stopped before the end.
- Focusing on small factors will improve the chances to be able to find a combination so that all the factors are square numbers.
The techniques of factorization into only small prime numbers evolved to smoothness detection tests. (Smoothness is friabilité in French, it means an integer which is the product of prime numbers smaller than a given bound. The prime numbers can have some power: 32 is 2-smooth because 32 = 25).
The step of finding a combination of the relations to obtain a square on the right is done with linear algebra: store the exponents in a matrix, actually store only if the exponent is odd or even (1 or 0 modulo 2), and compute the left kernel of the matrix. Linear algebra on very huge matrices is a research field in itself.
Limitations of the quadratic sieve
Complexity: exp(sqrt((2 + o(1)) ln N ln ln N))
- The integers to be factored into small primes are n = (a+m)2 – N of size about A sqrt(N) where A is the bound on the small integers a. For N larger than 100 decimal digits, it is not competitive.
- the smoothness bound determines the size of the linear system to solve: as we have seen, there are B/ln(B) prime numbers up to a bound B, hence keeping the relations where the right-hand side is B-smooth results in a linear system with a quite huge matrix, of B/ln(B) rows and columns. If B is not large enough, there will not be enough relations and no solution will be found.
- The aim is to find the best trade-off between A and B to minimize the cost of the algorithm.
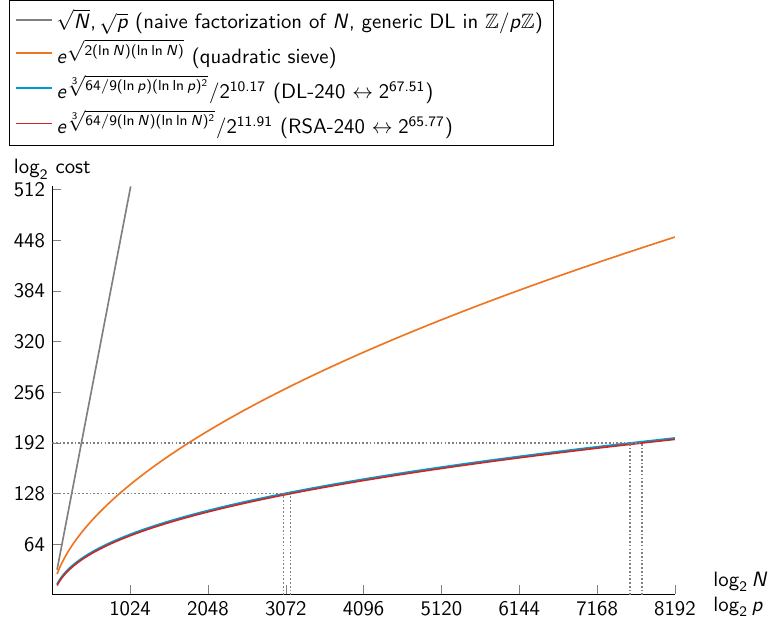
Graph of complexity of integer factorization and discrete logarithm with NFS, quadratic sieve, naive integer factorization, and generic DL computation
Nowadays’ method: the Number Field Sieve
(in French: Crible Algébrique)
The Number Field Sieve was developed in the 80’s and 90’s for integer factorization and discrete logarithm computation. Observing that the bottleneck of the quadratic sieve is the million of factorizations of numbers of the size of sqrt(N), the aim is to reduce the size of these numbers.
The mathematics involved in the Number Field Sieve are beyond the scope of this document. In short, there are two main steps: collecting many relations between smooth numbers, and then solving a very large sparse linear system.
The numbers to be factored are much smaller compared to the quadratic sieve. There are two small integers a and b (instead of one a in the quadratic sieve). The integers to factor are of size Ad N1/d where d is some degree between 3 and 6 in practical implementations, and A is a bound on a and b.
The linear system to solve is sparse. A sparse matrix has most of its entries set to zero. The average number of non-zero coefficients per row is called the density. In the case of a sparse matrix, computing a kernel costs about O(n2) where n is the number of rows and columns (for a square matrix).
Record computations
The latest record computation of factoring an RSA challenge was performed by the researchers Boudot, Gaudry, Guillevic, Heninger, Thomé and Zimmermann from France and US, with computing power in Europe and US. See Nouveaux records de factorisation et de calcul de logarithme discret for a presentation of the record computations in French.
Here is a figure to compare the record computations of Integer Factorization and Discrete Logarithm computation, and a table of the RSA number factorizations with the Number Field Sieve.
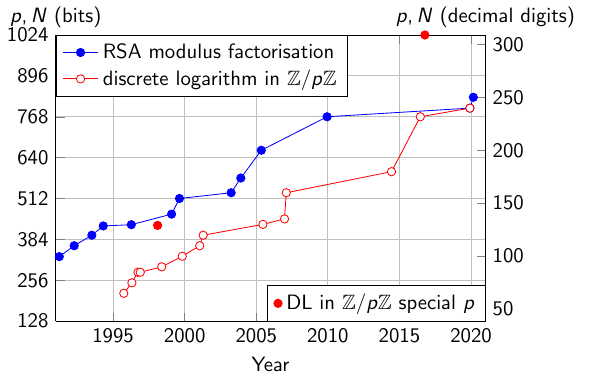
Record computations: RSA modulus factorization and discrete logarithm computation in prime fields.
| N | decimal digits | bits | Day | Authors |
|---|---|---|---|---|
| RSA-100 | 100 | 330 | April 1, 1991 | Lenstra |
| RSA-110 | 110 | 364 | April 14, 1992 | Lenstra, Manasse |
| RSA-120 | 120 | 397 | July 9, 1993 | Denny, Dodson, Lenstra, Manasse |
| RSA-129 | 129 | 426 | April 26, 1994 | Atkins, Graff, Lenstra, Leyland |
| RSA-130 | 130 | 430 | April 10, 1996 | Cowie, Dodson, Elkenbracht-Huizing, Lenstra, Montgomery, Zayer |
| RSA-140 | 140 | 463 | February 2, 1999 | Cavallar, Dodson, Lenstra, Leyland, Lioen, Montgomery, Murphy, te Riele, Zimmermann |
| RSA-512 | 155 | 512 | August 22, 1999 | Cavallar, Dodson, Lenstra, Lioen, Montgomery, Murphy, te Riele, Aardal, Gilchrist, Guillerm, Leyland, Marchand, Morain, Muffett, Putnam, Putnam, Zimmermann |
| RSA-160 | 160 | 530 | April 1, 2003 | Bahr, Franke, Kleinjung, Lochter, Böhm |
| RSA-576 | 174 | 576 | December 3, 2003 | Franke, Kleinjung, Montgomery, te Riele, Bahr |
| RSA-200 | 200 | 663 | May 9, 2005 | Bahr, Böhm, Franke, Kleinjung |
| RSA-768 | 232 | 768 | December 12, 2009 | Kleinjung, Aoki, Franke, Lenstra, Thomé, Bos, Gaudry, Kruppa, Montgomery, Osvik, te Riele, Timofeev, Zimmermann |
| RSA-240 | 240 | 795 | December 2, 2019 | Boudot, Gaudry, Guillevic, Heninger, Thomé, Zimmermann |
| RSA-250 | 250 | 829 | February 28, 2020 | Boudot, Gaudry, Guillevic, Heninger, Thomé, Zimmermann |
Integer factorization records since the RSA challenge, from Nouveaux records de factorisation et de calcul de logarithme discret, Boudot, Gaudry, Guillevic, Heninger, Thomé, Zimmermann, Techniques de l’ingénieur, 2020, à paraitre. Version prélimiaire ici See also RSA Factoring Challenge on Wikipedia.
Attacks on the RSA cryptosystem
A survey paper by Dan Boneh in 1999:
Too short keys: Humpich episode (1997 in France)
The story, in French (also, Le Monde 24.01.2000, page 8, 11.03.2000, 24.01.2001) After the affair, on March 4, 2000 the 96 decimal-digit key of GIE carte bancaire (groupement d’intérêt économique) was released on the internet. It was then possible for anyone with adequate hardware to forge yescards. (example of newspapers)
In 1997, the RSA keys were 320-bit long. It was already extremely short: the academic record factorization in 1996 was 130 decimal digits, which is 430 bits. 320 bits means 96 decimal digits, it is possible to factor such a number with the quadratic sieve.
Nowadays, the keys are still quite short: 1152 bits in 2020.
Wrong key sizes: Bitcrypt ransomware (2014)
Web Page (Airbus Cybersecurity, formerly Cassidian). In February 2014, a new ransomware named BitCrypt started to ransom random users. Two computer scientists in France, Fabien Perigaud and Cédric Pernet, investigated the first version of this malware. It searches for files on the disk such as pictures, generates an AES (symmetric) key en encrypts the picture with it. Then each symmetric key is encrypted with a unique RSA key. The malware claims a 1024-bit RSA encryption, but actually the RSA key was 31298847196625400639506938637161930162789011464295952600544145829335849533528834917800088971765784757175491347320005860302574523 of 128 decimal digits. This was a unit mistake: 1024 bits are 128 bytes (one byte is 8 bits), but 128 digits correspond to 426 bits.
With the free software cado-nfs, the two cryptographers Perigaud and Pernet were able to factor the RSA modulus: the two prime factors are p = 4627583475399516037897017387039865329961620697520288948716924853 and q = 6763540271723193027434512605129229364869394444394656022641769391. Then they obtained the secret RSA key to decipher the AES symmetric keys, and finally recovered the encrypted data. But one week later, the malware was updated with a new 1024-bit RSA key, which is out of reach for factorization.
Bad randomness: gcd, Coppersmith attacks
Gcd attack (2012, 2013)
We saw above that there are many distinct prime numbers of a given size: for a 2048-bit RSA modulus N (617 digits), there are about 21014, that is 10306 distinct prime numbers of 1024 bits (308-309 decimal digits). In other words, the set where to choose p and q is extremely large. It is large enough to generate billions of distinct RSA keys, as long as the randomness is of good quality: one need to be sure that no one will generate the same p independently.
In 2012 and 2013, different teams of researchers were able to obtain the private keys p and q of some rare public keys N by scanning the certificates on the internet, then computing massively gcd (greatest common divisor) over all the keys. They obtained gcd values larger than one, this is a factor of two distinct public keys! More precisely, they found that in some cases, two distinct keys N1 and N2 share one common factor p: N1 = pq1 and N2 = pq2. In such a case, the two public keys N1 and N2 can be easily factored.
Over a set of n RSA public keys of the same size, a naive computation of gcds of all pairs of keys requires n(n-1)/2 tests. To improve the runnung-time of this massive gcd computation, the authors used a technique called batch gcd. One multiplies together batches of RSA public keys before computing gcds.
- Nadia Heninger, Zakir Durumeric, Eric Wustrow, and J. Alex Halderman. Mining your Ps and Qs: Detection of widespread weak keys in network devices. In Tadayoshi Kohno, editor, USENIX Security 2012, pages 205-220. USENIX Association, August 2012. Video and paper
- Arjen K. Lenstra, James P. Hughes, Maxime Augier, Joppe W. Bos, Thorsten Kleinjung, and Christophe Wachter. Public keys. In Reihaneh Safavi-Naini and Ran Canetti, editors, CRYPTO 2012, volume 7417 of LNCS, pages 626-642. Springer, Heidelberg, August 2012. DOI 10.1007/978-3-642-32009-5_37 free IACR archive
Coppersmith attack (2013)
In cases where the randomness is bad or wrongly used, a Coppersmith attack can happen. It was the case in 2013 over a large set of ID cards in the Taiwan system of digital ID.
First steps: gcd attack and further pattern testings
- More than 2 million of 1024-bit RSA public keys (2 086 177)
- Batch gcd over the keys: 103 public keys factor into 119 different primes (one needs 206 distinct primes to generate 103 totally distinct RSA keys).
- Pattern found in the primes: there was no underlying proper use of a good random-number generator.
- Testing all primes following the expected pattern (164 primes) produced 18 more factorizations. Further investigation gave 4 more factorizations.
The most common prime factor (found in 46 distinct RSA modules) was p = 2511 + 2510 + 761 wich is the next prime after 2511 + 2510.
Next step: Coppersmith attack
Because of the function next_prime used in the (wrong) prime generation process, the least significant bits do not follow a pattern. However, when the most significants bits of a number N are known, Coppersmith’s technique allows to recover a factor of N.
The following SageMath code reproduces the example from the paper:
p = next_prime(2**511 + 2**510)
q = 0xc92424922492924992494924492424922492924992494924492424922492924992494924492424922492924992494924492424922492924992494924492424e5
N = p * q
X = 2**168
a = 0xc9242492249292499249492449242492249292499249492449242492249292499249492449242492249292499249492449242492249292499249492449242492
M = Matrix(3, 3, [X**2, X*a, 0, 0, X, a, 0, 0, N])
R = M.LLL()
g0 = R[0][2]
g1 = R[0][1] // X
g2 = R[0][0] // X**2
c = gcd([g0,g1,g2]) # gcd of coefficients
ZZx.<x> = ZZ[]
g = (g0 + g1*x + g2*x**2) // c
g.factor()
# (x - 83) * (30064312327*x - 23972510637500)
g(83) == 0
q == a + 83it works even if one of the primes is a good random-looking prime:
pi = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861
p = next_prime(floor(3*10**153 * pi))
# pattern
a = 0xabcdef1234567890abcdef1234567890abcdef1234567890abcdef1234567890abcdef1234567890abcdef1234567890abcdef1234567890abcdef1234567890
mask = 0x373487da48205b420e32198eb592f66ff4036668142 (a random-looking integer of 170 bits)
q = next_prime(a + mask)
N = p*q
X = 2**170
M = Matrix(3, 3, [X**2, X*a, 0, 0, X, a, 0, 0, N])
R = M.LLL()
g0 = R[0][2]
g1 = R[0][1] // X
g2 = R[0][0] // X**2
c = gcd([g0,g1,g2]) # gcd of coefficients
ZZx.<x> = ZZ[]
g = (g0 + g1*x + g2*x**2) // c
g.factor()
# (x - 1290919795022495591476339394838400757312676461707819) * (285540389921735875044941860691872438862439969180237*x - 2764078888444839645345836360217456914343392132618412376463107078920699665583816722965783600691378228578)
r = g.roots()[0][0]
q == a + r # True- Daniel J. Bernstein, Yun-An Chang, Chen-Mou Cheng, Li-Ping Chou, Nadia Heninger, Tanja Lange, and Nicko van Someren. Factoring RSA keys from certified smart cards: Coppersmith in the wild. In Kazue Sako and Palash Sarkar, editors, ASIACRYPT 2013, Part II, volume 8270 of LNCS, pages 341-360. Springer, Heidelberg, December 2013. DOI 10.1007/978-3-642-42045-0_18 free IACR archive
RSA and the quantum computer
If one day a powerful enough quantum computer exists, it will be able to break any RSA public key by factoring the modulus, but such a computer does not seem to come in the next ten years (we are in 2020). As said in Nouveaux records de factorisation et de calcul de logarithme discret:
In 1994, Peter Shor designed an algorithm for integer factorization with a quantum computer, which is much faster. The factorization of a n-bit integer requires a perfect quantum computer with 2n qbits (quantum bits). Such a computer seems extremely hard to build. The record computation is actually very small: in 2018, it was 4 088 459 = 2017 × 2027. And it is not clear that the factorization process can be adapted to any other integer of seven digits. To put a long story short, most probably RSA-1024 (in bits) will be factored before a quantum compter become competitive.
Diffie-Hellman, and the discrete logarithm problem
In the 70’s in the US, another cryptosystem was invented: the Diffie-Hellman key exchange (Merkle was also involved in the patent). This scheme is based on a different hard mathematical problem: the discrete logarithm problem.
Textbook Understanding cryptography, Chapters 6 and 7.
Handbook of applied cryptography, sections 3.6 and 3.7 of chapter 3 and section 8.4 of chapter 8.
Discrete logarithm problem and cryptosystems
Discrete logarithm problem
The discrete logarithm problem is usually stated as follows. Given a multiplicative group G of order r, a generator g of the group and an element h in G, find an integer x such that h = gx. Because this x is a preimage for the exponentiation in G, and it takes integer values, it is called a discrete logarithm.
For example, consider the prime number of 1024 bits in OAKLEY IETF
p = 179769313486231590770839156793787453197860296048756011706444423684197180216158519368947833795864925541502180565485980503646440548199239100050792877003355816639229553136239076508735759914822574862575007425302077447712589550957937778424442426617334727629299387668709205606050270810842907692932019128194467627007
p is prime, and q = (p-1)/2 is prime too: p is a Sophie Germain prime (named after the French mathematician Sophie Germain), also known as a safe prime. p has no particular form and was generated from the decimals of π: p = 21024 – 2960 – 1 + 264 · ([2894 · π] + 129093)
pi = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861
p = 2**1024 - 2**960 - 1 + 2**64 * (floor(2**894 * pi) + 129093)A generator is g = 2 of order q (it is not of order p-1 but (p-1)/2).
Given the public parameters p, q and g, it is fast to compute a modular exponentiation ga mod p, where a is an integer between 1 and q-1. It is called a binary exponentiation: one reads the binary representation of a and computes squares and multiplications modulo p to obtain ga. It requires in average n squarings and n/2 multiplications modulo p (the numbers never grow, they are always in 1, …, p -1). A simple square-and-multiply in Python looks like:
from random import randrange
p = 179769313486231590770839156793787453197860296048756011706444423684197180216158519368947833795864925541502180565485980503646440548199239100050792877003355816639229553136239076508735759914822574862575007425302077447712589550957937778424442426617334727629299387668709205606050270810842907692932019128194467627007
q = (p-1)//2
g = 2
a = randrange(1, q)
gi = g
if (a % 2) == 1:
h = g
else:
h = 1
ai = a // 2
while ai > 0:
gi = g**2 % p
if (ai % 2) == 1:
h = (h * gi) % p
ai = ai // 2But it is a very hard mathematical problem to inverse this function, that is, to compute a when knowing only p, q, g and h where h was computed as ga.
Choice of group
The first choices of groups G where finite fields of two kinds:
- Prime finite fields denoted Z/pZ or Fp where p is a prime number. This notation says that the arithmetic is done modulo p (in Python or C, a reduction modulo an integer is denoted
a % b). Considering the multiplication, the number 0 is discarded, all integers from 1 to p-1 are considered: {1, 2, …, p-1}. When multiplying or dividing two numbers in this set, the operation is followed by a reduction modulo p, so that the result is always in the set of numbers from 1 to p-1.
But because of mathematical algorithms to compute discrete logarithms, this is the same problem as for the RSA cryptosystem: the size of p should be large (at least 2048 bits). - Finite fields of characteristic 2. It means, defining a group of order 2n. But this is not « computing modulo 2n« . It means: choosing an irreducible polynomial of degree n and coefficients in {0, 1}. This field is denoted F2n (in French) and GF(2n) for Galois Field (in English). For example, with n = 127 (it is a prime), one defines f(x) = x127 + x + 1 an irreducible polynomial (it does not factor into polynomials of smaller degree). An element in GF(2127) is a vector of bits 0, 1 of length 127, it corresponds to the coefficients of a polynomial of degree 126. v = [v0, v1, …, v126] and v = v0 + v1x + … + v126x126. The addition is done coefficient-wise, like the addition of two vectors. But because we are modulo 2, we have 1+1 = 2 = 0 mod 2, hence the coefficients are always in {0, 1}. In software (such as C), one can encode the coefficients directly as unsigned integers in binary representation, and the addition coefficient-wise is a XOR, there is no carry. To store an element of GF(2127), one needs two machine-words of 64 bits for example. In particular, the multi-precision arithmetic is much easier compared to Z/pZ, because there is no carry propagation in the arithmetic. For the multiplication, one way is to use look-up tables pre-computed according to the choice of the irreducible polynomial.
In other well-chosen groups G, computing a discrete logarithm is a very hard problem; only generic algorithms apply. They have a complexity linear in the square root of the order of the group, denoted O(sqrt(# G)), where # G is the order of the group. Nowadays, the preferred group is the group of points of an elliptic curve, and one widely deployed example is the curve named ed25519.
Elliptic curves were introduced in cryptography in 1985 by Koblitz and Miller. The addition law of the group of points is depicted in the following Figure. The elements of this group G are coordinates (x,y) in Fp × Fp satisfying a curve equation of the form y2 = x3 + a · x + b with parameters a, b in the finite field Fp. The addition of to points P(x1, y1) and Q(x2, y2) has a geometric meaning, with the chord and tangent construction. In this case the group has an additive notation. The exponentiation takes as input an integer x and a point P, and computes x · P.
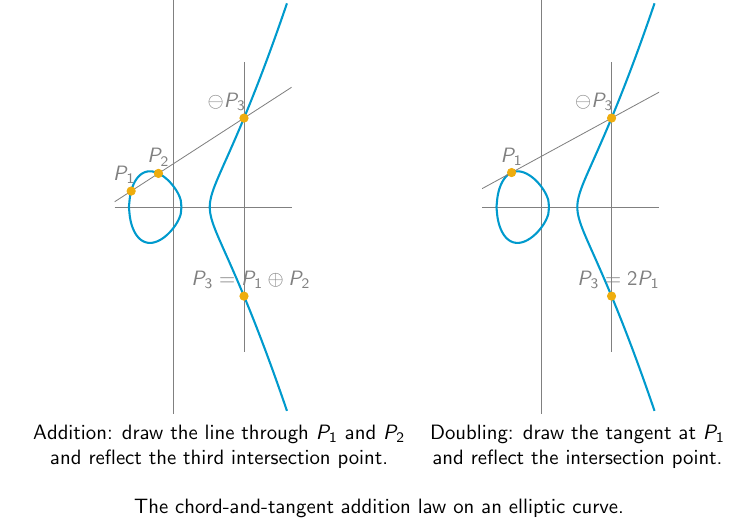
The hardness of the discrete logarithm problem (inverting the exponentiation) on elliptic curves is well-investigated since 1985. Computing a discrete logarithm on the group G of points of an elliptic curve is done with generic techniques of complexity O(sqrt(# G)). It has not changed since its introduction in cryptography in 1985 (except for well-identified rare curves that are easy to avoid). To ensure a 128-bit security level to match the well-deployed AES-128 (with 128-bit keys), one chooses a group on a curve of prime order of 256 bits. For example, the curve named ed25519 is an elliptic curve in Edwards form over the prime field Fp with p = 2255-19, hence of 256 bits, and the curve has order 8 · r where r is a prime of 253 bits. It offers 128 bits of security. Elliptic curve standards (IEEE 1363, FIPS 186.2, SECG) recommend the use of elliptic curves with group order h · r, where r is a prime and the cofactor h is an integer between 1 and 4.
In more detail, to ensure that an attack computing a discrete logarithm in a well-chosen elliptic curve will take at least 2n operations (as much as a brute-force search for a symmetric cipher with a key of n bits), one chooses a key of value near 22n, that is of size 2n bits: then sqrt(22n) = 2n (usually the time unit is some basic operation involved).
Diffie-Hellman key exchange
The two participants are again Alice and Bob.
- First they agree on the public parameters p, q and a generator g of order q.
- Then separately, Alice chooses her private key a as a random number in the set {1, …, q-1} and computes her public key A = ga mod p, and Bob chooses b randomly in the same set and computes B = gb mod p.
- Alice sends A to Bob and Bob sends B to Alice on an insecure channel. None of a or b were sent explicitly. They are hidden in the exponents.
- Alice computes Ba and Bob computes Ab. Now they share the same secret data S = gab. It can be used to derive a symmetric key (to use with a symmetric cipher such as AES) and encrypt the following of the exchange between Alice and Bob.
Alice cannot compute Bob’s private key, nor Bob can compute Alice’s private key. No one knowing the public parameters and the public data A and B can compute the secret keys or the shared secret: with A and B, one can only compute ga+b, but not gab.
ElGamal, Schnorr signature, DSA
- ElGamal encryption, textbook (Paar Pelzl) Chapter 8 section 5 page 226, Handbook of Applied Cryptography Chapter 8 section 4 (8.4), on Wikipedia;
- ElGamal signature scheme, textbook (Paar Pelzl) Chapter 10 section 3 page 270, Handbook of Applied Cryptography Chapter 11 section 5.2 (11.5.2),
- Schnorr signature, patented until February 2008, on Wikipedia
- Digital Signature Algorithm (DSA), textbook (Paar Pelzl) Chapter 10 section 4 page 277, Handbook of Applied Cryptography Chapter 11 section 5.1 (11.5.1), on Wikipedia, NIST FIPS 186-4 Section 4
- ECDSA (elliptic curve DSA), textbook (Paar Pelzl) chapter 10 section 5 (10.5 page 282), NIST FIPS 186-4 Section 6
Computing discrete logarithms
The RSA cryptosystem and the Diffie-Hellman cryptosystems were developed at the same time in cryptography, starting in the mid 70’s. Finding better algorithms for integer factorization and discrete logarithm computation were also developed together. The best algorithms for these two problems on large cryptographic parameters are two variants of the Number Field Sieve algorithm, of same complexity. In Nancy since 2007, a software is developed and handles both cases. Unfortunately it is poorly documented, but it holds the latest (academic) record computations for the two problems. The latest records are the factorization of the challenge RSA-250 (in decimal digits, corresponding to 829 bits) in February 2020, and a discrete logarithm computation in a prime field of 240 decimal digits (795 bits) in December 2019.
The research on discrete logarithm computation has been continuous since its use in cryptography.
Laurent Grémy (Quarkslab) maintains a web page of record computations: The Discrete Logarithm Database. The following table is obtained from this database.
| bits | decimals | Date | Authors | Link | Comment |
|---|---|---|---|---|---|
| 215 | 65 | 02/10/1995 | Damian Weber, Thomas Denny and Joerg Zayer | nmbrthy | |
| 248 | 75 | 25/04/1996 | Damian Weber, Thomas Denny and Joerg Zayer | nmbrthy | |
| 281 | 85 | 25/09/1996 | Damian Weber, Thomas Denny and Joerg Zayer | nmbrthy | |
| 281 | 85 | 25/11/1996 | Damian Weber, Thomas Denny and Joerg Zayer | nmbrthy | |
| 427 | 129 | 25/02/1998 | Damian Weber and Thomas Denny | nmbrthy DOI | Special p, Joerg Zayer was involved in a first step of the computation (see nmbrthy) |
| 298 | 90 | 26/05/1998 | Antoine Joux and Reynald Lercier | nmbrthy | |
| 331 | 100 | 01/11/1999 | Antoine Joux and Reynald Lercier | ECC’99, Waterloo slides | |
| 364 | 110 | 19/01/2001 | Antoine Joux and Reynald Lercier | nmbrthy | |
| 397 | 120 | 17/04/2001 | Antoine Joux and Reynald Lercier | nmbrthy | |
| 431 | 130 | 18/06/2005 | Antoine Joux and Reynald Lercier | nmbrthy | |
| 448 | 135 | 22/12/2006 | Andrey Dorofeev, Denis Dygin and Dmitry Matyukhin | nmbrthy | |
| 530 | 160 | 05/02/2007 | Thorsten Kleinjung | nmbrthy | |
| 596 | 180 | 11/06/2014 | Cyril Bouvier, Pierrick Gaudry, Laurent Imbert, Hamza Jeljeli and Emmanuel Thomé | nmbrthy | |
| 512 | 20/05/2015 | David Adrian, Karthikeyan Bhargavan, Zakir Durumeric, Pierrick Gaudry, Matthew Green, J. Alex Halderman, Nadia Heninger, Drew Springall, Emmanuel Thomé, Luke Valenta, Benjamin VanderSloot, Eric Wustrow, Santiago Zanella-Béguelin and Paul Zimmermann | DOI | Logjam attack | |
| 768 | 232 | 16/06/2016 | Thorsten Kleinjung, Claus Diem, Arjen Lenstra, Christine Priplata and Colin Stahlke | nmbrthy DOI | |
| 1024 | 309 | 10/10/2016 | Joshua Fried, Pierrick Gaudry, Nadia Heninger and Emmanuel Thomé | nmbrthy DOI | Special p |
| 795 | 240 | 02/12/2019 | Fabrice Boudot, Pierrick Gaudry, Aurore Guillevic, Nadia Heninger, Emmanuel Thomé and Paul Zimmermann | nmbrthy DOI |
Generic algorithms of square root complexity
- Shanks algorithm baby-step-giant-step (BSGS) has complexity O(sqrt(#G)), and is deterministic. It requires large amount of memory.
- A variant is a random walk in G, then computing a discrete logarithm is like finding a cycle path in a connected graph (for this, there is Floyd’s algorithm). Applied to G, this is Pollard’s algorithm, of complexity O(sqrt(#G)), probabilistic, and much less memory is needed.
- Other time-memory trade-offs are possible, with parallel searches (parallel Pollard, Kangaroos)
If the factorization of the order of G is known:
- the Pohlig-Hellman algorithm applies: it runs an independent search in each distinct subgroup and uses the Chinese Remainder Theorem (CRT) to combine the answers. Complexity: O(sqrt(r)) for each prime factor r of #G, the largest prime r matters: that is why G is taken of prime order (or, a tiny number times a prime).
Index calculus algorithm
It was introduced by Western and Miller in 1968 and Adleman in 1979.
Let p be a prime number, and q = (p – 1)/2 (or q = (p – 1)/4) be a prime. Let G = Z/pZ and let g be a generator of the multiplicative sub-group. Let h be the target: we aim at computing x such that gx = h.
- Get many multiplicative relations between elements of G:
gt = g1e1 g2e2 ⋯ giei mod p
where t is a known integer, and g1, g2, …, gi are elements of G. - Obtain a relation involving the target h: try many s until
h · gs = g1e‘1 · g2e‘2 ⋯ gie‘i mod p - Consider the exponents, that is, takes the logarithms in basis g: one obtains linear relations modulo p – 1:
t = e1 logg g1 + e2 logg g2 + … ei logg gi mod p – 1
…
loggh + s = e‘1 logg g1 + e‘2 logg g2 + … ei‘ logg gi mod p – 1 - Solve a linear system modulo p – 1
- get x = logg h
Numerical example: p = 1109, q = (p – 1)/4 = 277 is prime. Consider the prime integers 2, 3, 5, 7, 11, 13 for the gi.
- Consider successive integers t starting at 2 and until six relations are found, because there are six integers gi of unknown logarithm. We start with g = 2 to ensure that the logarithms are in basis g.
g1 = 2
g13 = 429 = 3 · 11 · 13
g16 = 105 = 3 · 5 · 7
g21 = 33 = 3 · 11
g44 = 1029= 3 · 73
g72 = 325 = 52 · 13 - With the target h = 777, one finds that g10 · h = 495 = 32 · 5 · 11 mod p.
- Solving the system modulo q then p – 1 gives logg 2 = 1, logg 3 = 219, logg 5 = 594, logg 7 = 311, logg 11 = 910, logg 13 = 1100.
- Finally, logg h = -10 + 2 logg 3 + logg 5 + logg 11 = 824 mod p – 1. Indeed, one can check that g824 = 777 mod p.
Quadratic Sieve, Number Field Sieve
In 1986, Coppersmith, Odlyzko, and Schroeppel published the quadratic sieve. Is introduces a technique of sieving to avoid a complete factorization of non-promising numbers. It detects the smooth integers. Then, they can be factored into prime factors. The non-smooth integers are not factorized at all. However, it requires the space to store in memory (in RAM) all the numbers.
In 1985, ElGamal designed an algorithm to compute discrete logarithms in GF(p2) with two quadratic number fields. In 1986, Coppersmith, Odlyzko, and Schroeppel applied it to GF(p). It allowed a more mathematical way to look at the index calculus technique. It introduces the use of a quadratic number field. For example, the complex numbers a + b i where i2 = -1, and with a and b rational numbers (in Q), is a number field.
It was then possible to generalize the algorithm to more general number fields. The idea was applied to the factorization of integers. Right after, in 1993, Gordon published the number field sieve algorithm for computing discrete logarithms in prime fields. The complexity was improved by Schirokauer the same year, and it is nowadays the same complexity. The algorithm was continuously improved in practice until now, but the asymptotic complexity did not change.
Choosing key-sizes
The website keylength.com lists the recommendations from different agencies.
Attacks on discrete-logarithm based cryptosystems
Sony Play-Station 3 (PS3) hacking
It was a problem of bad randomness in the ECDSA signature Slides of the talk at CCC 122-134 (Chaos Communication Congress, every year in Germany). The same random token was used to sign everything. It means with two public signatures, one can recover the private key and then sign anything with this private key.
ECDSA signature
(From textbook Paar Pelzl, Chapter 10 section 5)
ECDSA (Elliptic Curve Digital Signature Algorithm) needs an elliptic curve E defined over a prime field GF(p) (it works for other types of fields, in particular GF(2n), Koblitz curves and binary curves). Assume the curve has a sub-group of large prime order q and a generator is given as a point G(xG,yG).
Public Parameters
- p
- Elliptic curve E (coefficients of the curve equation)
- group order q (prime)
- generator of order q: G=(xG,yG)
Key generation
- Choose a random integer d in {1, …, q – 1}
- Compute the point P = d · G
- Public key: (p, q, E (coefficients), G, P)
- Private key: (d)
Signing of a message m:
- Choose an ephemeral private key as an integer ke in {1, …, q – 1}.
- Compute the point R = ke · G
- Let r = xR the x-coordinate of the point R.
- Compute s = (H(m) + d · r) · ke-1 mod q where H is a cryptographic hash function whose output is at least of the same length as of q (for example, 256 bits or 32 bytes).
The signature is (r, s).
Verification
- Compute w = s-1 mod q
- Compute u1 = w · H(m) mod q (with the same hash function H)
- Compute u2 = w · r mod q
- Compute Q = u1 · G + u2 · P (a point on E)
- if xQ = r mod q then the signature is valid,
otherwise the signature is invalid.
PS3 problem
The hackers discovered that the same ephemeral key ke was used to sign different things. They were able to obtain the data for distinct messages, say m1 and m2. It consists in
- (r, s1 = (H(m1) + d · r) · ke-1 mod q)
- (r, s2 = (H(m2) + d · r) · ke-1 mod q)
One wants to recover the private key d. Observe that
s1 – s2 mod q = (H(m1) + d · r) · ke-1 – (H(m2) + d · r) · ke-1 = (H(m1) – H(m2)) · ke-1 mod q
The secret key d vanished! We can publicly compute h = H(m1) – H(m2) mod q, then recover the (actually non-ephemeral) key ke.
- h = H(m1) – H(m2) mod q
- ke = h / (s1 – s2) mod q
- d = (s1 · ke – H(m1)) / r mod q
Knowing the manufacturer’s private key d allows to sign non-legitimate documents (software, games for the PS3), and the signature will be accepted as a valid signature by any verifier.
Weak DH attack
- David Adrian, Karthikeyan Bhargavan, Zakir Durumeric, Pierrick Gaudry, Matthew Green, J. Alex Halderman, Nadia Heninger, Drew Springall, Emmanuel Thomé, Luke Valenta, Benjamin VanderSloot, Eric Wustrow, Santiago Zanella-Béguelin, and Paul Zimmermann. Imperfect forward secrecy: How Diffie-Hellman fails in practice. In 22nd ACM Conference on Computer and Communications Security, October 2015. url.
Weak keys in the Moscow internet voting system
Discrete logarithm computation in finite fields F2n = GF(2n) and F3m = GF(3m)
For better hardware efficiency, finite fields F2n = GF(2n) were introduced in cryptography. But already in 1984, it was known that computing a discrete logarithm was easier in these fields, that is, for a same size (a field GF(2n) has n bits, a prime field GF(p) has size the number of bits of p), it was much faster to compute a discrete logarithm in GF(2n), because these kind of fields have more structure. In 1984, Blake, Fuji-Hara, Mullin, Vanstone in two papers, and Coppersmith in a third paper showed how to compute discrete logarithms in GF(2127).
- Blake, I.F., Fuji-Hara, R., Mullin, R.C., Vanstone, S.A.: Computing logarithms in finite fields of characteristic two. SIAM Journal on Algebraic Discrete Methods 5(2), pages 276-285 (1984). DOI 10.1137/0605029
- Blake, I.F., Mullin, R.C., Vanstone, S.A.: Computing logarithms in GF(2n). In: Blakley, G.R., Chaum, D. (eds.) CRYPTO’84. LNCS, vol. 196, pp. 73-82. Springer, Heidelberg (Aug 1984). DOI 10.1007/3-540-39568-7_8
- Coppersmith, D.: Fast evaluation of logarithms in fields of characteristic two. IEEE Transactions on Information Theory 30(4), pages 587-594 (1984). DOI 10.1109/TIT.1984.1056941
The following graph shows the record computations in finite fields of the form GF(2n) and GF(3m), except for the latest record in GF(230750) that is outside of the scale. The data is extracted from dldb.
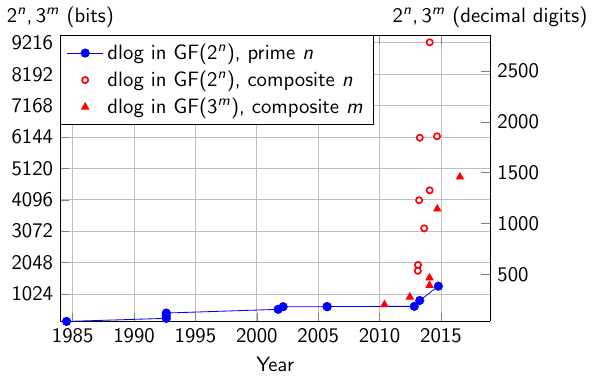
| field | bits | decimals | Date | Authors | Link | Comment |
|---|---|---|---|---|---|---|
| 230750 | 30750 | 9257 | 10/07/2019 | Robert Granger, Thorsten Kleinjung, Arjen Lenstra, Benjamin Wesolowski and Jens Zumbrägel | nmbrthy ePrint | Kummer extension |
| 33054 | 4841 | 2310 | 18/07/2016 | Gora Adj, Isaac Canales-Martinez, Nareli Cruz-Cortés, Alfred Menezes, Thomaz Oliveira, Luis Rivera-Zamarripa and Francisco Rodriguez-Henriquez | nmbrthy DOI | |
| 21279 | 1279 | 386 | 17/10/2014 | Thorsten Kleinjung | nmbrthy | Prime extension |
| 32395 | 3796 | 1812 | 15/09/2014 | Antoine Joux and Cécile Pierrot | nmbrthy DOI | |
| 29234 | 9234 | 2780 | 31/01/2014 | Robert Granger, Thorsten Kleinjung and Jens Zumbrägel | nmbrthy | Kummer extension |
| 24404 | 4404 | 1326 | 30/01/2014 | Robert Granger, Thorsten Kleinjung and Jens Zumbrägel | nmbrthy DOI | |
| 3978 | 1551 | 741 | 26/01/2014 | Gora Adj, Alfred Menezes, Thomaz Oliveira and Francisco Rodriguez-Henriquez | DOI | |
| 3822 | 1303 | 622 | 26/01/2014 | Gora Adj, Alfred Menezes, Thomaz Oliveira and Francisco Rodriguez-Henriquez | DOI | |
| 23164 | 3164 | 953 | 21/08/2013 | Faruk Göloğlu, Robert Granger, Gary McGuire and Jens Zumbrägel | DOI | Kummer extension |
| 26168 | 6168 | 1857 | 21/05/2013 | Antoine Joux | nmbrthy | Kummer extension |
| 26120 | 6120 | 1843 | 11/04/2013 | Faruk Göloğlu, Robert Granger, Gary McGuire and Jens Zumbrägel | nmbrthy | Kummer extension |
| 2809 | 809 | 244 | 09/04/2013 | Razvan Barbulescu, Cyril Bouvier, Jérémie Detrey, Pierrick Gaudry, Hamza Jeljeli, Emmanuel Thomé, Marion Videau and Paul Zimmermann | nmbrthy DOI | Prime extension |
| 24080 | 4080 | 1229 | 22/03/2013 | Antoine Joux | nmbrthy | Kummer extension |
| 21971 | 1971 | 594 | 19/02/2013 | Faruk Göloğlu, Robert Granger, Gary McGuire and Jens Zumbrägel | nmbrthy DOI | Kummer extension |
| 21778 | 1778 | 536 | 11/02/2013 | Antoine Joux | nmbrthy | Kummer extension |
| 2619 | 619 | 187 | 29/10/2012 | Razvan Barbulescu, Cyril Bouvier, Jérémie Detrey, Pierrick Gaudry, Hamza Jeljeli, Emmanuel Thomé, Marion Videau and Paul Zimmermann | ECC2012 | Prime extension |
| 3582 | 923 | 441 | 18/06/2012 | Takuya Hayashi, Takeshi Shimoyama, Naoyuki Shinohara and Tsuyoshi Takagi | DOI | |
| 3426 | 676 | 323 | 26/05/2010 | Takuya Hayashi, Naoyuki Shinohara, Lihua Wang, Shin’ichiro Matsuo, Masaaki Shirase and Tsuyoshi Takagi | DOI | |
| 2613 | 613 | 185 | 23/09/2005 | Antoine Joux and Reynald Lercier | nmbrthy | Prime extension |
| 2607 | 607 | 183 | 23/09/2005 | Antoine Joux and Reynald Lercier | nmbrthy | Prime extension |
| 2607 | 607 | 183 | 23/02/2002 | Emmanuel Thomé | nmbrthy | Prime extension |
| 2521 | 521 | 157 | 25/09/2001 | Antoine Joux and Reynald Lercier | nmbrthy | Prime extension |
| 2401 | 401 | 121 | 16/08/1992 | Daniel Gordon and Kevin McCurley | DOI | Prime extension |
| 2313 | 313 | 95 | 16/08/1992 | Daniel Gordon and Kevin McCurley | DOI | Prime extension |
| 2227 | 227 | 69 | 16/08/1992 | Daniel Gordon and Kevin McCurley | DOI | Prime extension |
| 2127 | 127 | 39 | 01/07/1984 | Don Coppersmith | DOI | Prime extension |
(The following summary of historical steps is from Chapter 9 Discrete Logarithms in Guide to pairing-based cryptography), a free archive is on HAL.
In 1984, Blake, Fuji-Hara, Mullin, and Vanstone proposed a dedicated implementation of Adleman’s algorithm in GF(2127). They introduced the idea of systematic equations, a very efficient way to generate relations thanks to the structure of the field (in that field, (x+y)2 = x2 + y2 modulo 2) and initial splitting (the name of their technique was introduced later). Their idea works for finite fields like GF(2n) and n is close to a power of 2 (e.g., 127 = 27 – 1). The asymptotic complexity of their method was exp(sqrt((2+o(1)) ln 2n ln ln 2n)). In the same year, Blake, Mullin, and Vanstone proposed an improved algorithm known as the Waterloo algorithm (it is a city in Ontario, Canada where is a famous university for computer science and electrical engineering, the author of the Handbook of applied cryptography is professor at the university of Waterloo). Odlyzko computed the asymptotic complexity of this algorithm in a paper published at the conference Eurocrypt’84 DOI. Coppersmith published the first record computation of a discrete logarithm in GF(2127) in 1984 and designed an algorithm of much better asymptotic complexity: exp((c+o(1)) (ln 2n)1/3 (ln ln 2n)2/3) for a constant c between 1.526 and 1.587. His idea was generalized to other finite fields but with a larger constant c. There was no significant improvement until the rise of finite fields coming with pairing-friendly curves in 2000 (see the following sections). The latest record computation took place in GF(230750) in 2019, that is, the discrete logarithm problem is easy in fields GF(2n) and GF(3m) for n, m composite, and it is impossible to build any secure cryptosystem in these cases.
In the case of pairing-friendly curves, with GF(2n), the extension degree n is a multiple of 4, and with GF(3m), m is a multiple of 6. This is an important property that made a big difference with the classical case where n and m are prime.
In 2010, the record computation was in GF(36 · 71) of 676 bits (323 decimal digits), made by a Japanese team. In 2012, they improved their record to GF(36 · 97) of 923 bits (441 decimal digits). In addition to the improvements of the techniques, the record was also made possible thanks to the increasing computing power. This announcement had a quite important effect over the community at that time, probably because the broken curve was the one used in the initial paper on short signatures from pairings (Asiacrypt’01, Boneh Lynn Shacham). The broken finite field GF(36 · 97) was the target field of a pairing-friendly elliptic curve defined over GF(397), considered safe in 2001 for 80-bit security implementations. Here are the press release (accessible to non-specialists) and the publications (more technical).
- Fujitsu Laboratories, NICT, and Kyushu University. DL record in F36 · 97 of 923 bits (278 decimal digits). NICT press release, June 18, 2012. NICT page
- Takuya Hayashi, Naoyuki Shinohara, Lihua Wang, Shin’ichiro Matsuo, Masaaki Shirase, and Tsuyoshi Takagi. Solving a 676-bit discrete logarithm problem in GF(36n). In P. Q. Nguyen and D. Pointcheval, editors, Public Key Cryptography – PKC 2010, volume 6056 of LNCS, pp. 351-367. Springer, Heidelberg, 2010. DOI 10.1007/978-3-642-13013-7_21
- Takuya Hayashi, Takeshi Shimoyama, Naoyuki Shinohara, and Tsuyoshi Takagi. Breaking pairing-based cryptosystems using etaT pairing over GF(397). In X. Wang and K. Sako, editors, ASIACRYPT 2012, vol. 7658 of LNCS, pp. 43–60. Springer, Heidelberg, 2012. DOI 10.1007/978-3-642-34961-4_5
At Christmas 2012, Joux proposed a conjectured heuristic algorithm of asymptotic complexity with an exponent 1/4 instead of 1/3: exp((c+o(1)) (ln 2n)1/4 (ln ln 2n)3/4) and announced two records of much larger size. The years 2013 and 2014 were very intense in improvements and record computations and in 2014, two algorithms of quasi polynomial time complexity were published. A major mathematical proof required in the algorithms was published in 2019. And the latest record computation is extremely large, of 30750 bits.
Pairings
What is a pairing?
A pairing (couplage in French) is a bilinear map that takes as input two points P=(x1, y1), Q=(x2, y2) on an elliptic curve E defined over a field Fq, and outputs a value in the finite field Fq<sup_k_. It is denoted
e: G1 × G2 → G3
where G1 and G2 are subgroups of E and G3 is a subgroup of Fq<sup_k_. The map is
- bilinear: e(P1 + P2, Q) = e(P1, Q) · e(P2, Q) and
e(P, Q1 + Q2) = e(P, Q1) · e(P, Q2); - non-degenerate: one cannot have e(P,Q) = 1 unless one of P, Q is the neutral element of the curve;
- efficiently computable.
In practice, the important property is the following: one can swap the discrete logarithm values and multiply them in the exponent: with two points P and Q and integers a and b, we have the equality:
e(aP, bQ) = e(bP, aQ) = e(P, Q)ab
Pairings in cryptography: 1993 and 2001
1993
Elliptic curves were introduced in 1985 for public-key cryptography. To use a curve as a group G for Diffie-Hellman (or any other discrete logarithm based cryptosystem), on needs to know the order of the curve. For a finite field Z/pZ where p is a prime, the order of the multiplicative group is p -1 because one removes zero and works with the set of integers {1, 2, 3, …, p – 1}. But for a curve, it is not the same. Its order can be any integer between p – 2 · sqrt(p) and p + 2 · sqrt(p). At that time, it was very hard to compute the exact number of points on the curve, and to bypass this difficulty, supersingular curves were used instead.
Supersingular curves have an equation of the form
- Ep: y2 = x3 + x over a prime field Fp where p modulo 4 is equal to 3, its order is p + 1 and G3 = Fp2;
- Ep: y2 = x3 + 1 over a prime field Fp where p modulo 3 is equal to 2, its order is p + 1 and G3 = Fp2;
- E3,1: y2 = x3 – x + 1 or E3,-1: y2 = x3 – x – 1 over a field F3m with odd m. Its order is 3m + 3(m+1)/2 + 1 or 3m – 3(m+1)/2 + 1 (depending on the choice of the coefficient 1 or -1) and G3 = F36 · m;
- E2,1: y2 + y = x3 + x + 1 or E2,0: y2 + y = x3 + x over a field F2n with odd n. Its order is 2n + 2(n+1)/2 + 1 or 2n – 2(n+1)/2 + 1 and G3 = F24 · n.
These curves were easy to generate: for curves over Fp, the aim is to find a prime p such that p+1 = 4 · r with r a prime for the first curve, and p+1 = 6 · r with r prime for the second curve. For the curves over F2n and F3m, the aim is to find n, or m such that the order of the curve is prime, or a tiny factor times a prime. For this, this is well documented that the order of the curve is the an Aurifeuillean factor:
- Define P6(x) = x2 – x + 1 the 6-th cyclotomic polynomial, we have P6(x) · (x+1) = x3+1, P6(3x2) = (3x2 – 3x + 1) · (3x2 + 3x + 1), and P6(3x2) divides (3x2)3+1. Now one looks at the Cunningham tables and search for a known factorization of 33(2b+1)+1.
- Define P4(x) = x2 + 1 the 4-th cyclotomic polynomial, we have P4(2x2) = (2x2 – 2x + 1) · (2x2 + 2x + 1), and P4(2x2) = (2x2)2+1. Now one looks at the Cunningham tables and search for a known factorization of 22(2a+1)+1.
In 1993, Menezes, Okamoto and Vanstone with the Weil pairing then Frey and Rück in 1994 with the Tate pairing showed that it is possible to compute discrete logarithms in a finite field Fp2 instead of an elliptic curve, that is, transferring the computation in G3. But if it is much easier to compute a discrete logarithm in G3, then this is a big failure in the system. Indeed, it was known from 1984 that a discrete logarithm in fields of the form F2n is much easier (for a same total size).
For Fp2, this is a problem of size of p. To ensure a security level of 80 bits of security on the elliptic curve (in 1993), a prime p of 160 bits was chosen, and a curve E of order q of 160 bits. If the curve is supersingular, then G3 = Fp2 and this field has size 320 bits. The algorithm of ElGamal applies (a quadratic sieve-like algorithm) and has complexity in exp(sqrt(48 · ln p · ln ln p)). It was not practical at that time, but in 1993, another algorithm was found for prime fields Fp of much better complexity (Gordon, exp((64/9 · ln p · (ln ln p)2)1/3)) and it was only a matter of time before his algorithm was adapted to fields Fp2 (Joux Lercier Smart Vercauteren in 2006, and in 2015, Barbulescu Gaudry Guillevic Morain showed that computing a discrete logarithm in Fp2 is easier than in a prime field Fq of same total size).
The big impact was for supersingular curves over F2n and F3m. In that case, Coppersmith’s algorithm applies and is practical and implemented since 1984. Its complexity is exp((32/9 · ln 2l · ln ln 2l)1/3) and replacing l by 4n, one obtains roughly 256, that is, the security is 56 bits (like the old DES) instead of 80 bits.
As a consequence, supersingular curves were avoided.
- Menezes, A., Okamoto, T., Vanstone, S.A.: Reducing elliptic curve logarithms to logarithms in a finite field. IEEE Transactions on Information Theory 39(5), pages 1639-1646 (1993). DOI 10.1109/18.259647
- Frey, G., Rück, H.G.: A remark concerning m-divisibility and the discrete logarithm in the divisor class group of curves. Mathematics of Computation 62(206), pages 865-874 (1994). DOI 10.1090/S0025-5718-1994-1218343-6
2001
In the 90’s, researchers worked on an efficient way of computing pairings. In 2000, Joux, based on previous works, was able to obtain an algorithm to compute very efficiently a pairing, in the spirit of a scalar multiplication on the curve. Many improvements followed, and in 2005, a very popular curve was found by Barreto and Naehrig (BN curve).
In 2000, Joux together with his efficient algorithm, proposed a key-exchange like a Diffie-Hellman key-exchange but with three participants. His idea needs an elliptic curve with a pairing. The important point is the choice of the curve: to ensure the same security level in the three groups G1, G2 and G3.
Joux’ tri-partite key exchange.
First, the three participants agree on public parameters: an elliptic curve E with an efficient pairing, a base point (generator) P for G1, a base point Q for G2. The three groups Gi are all of prime order r.
-
- Alice chooses a random integer a in {1, …, r – 1}, computes aP and sends it to Bob and Charlie;
- Bob chooses a random integer b in {1, …, r – 1}, computes bP, bQ and send bP to Alice and bQ to Charlie;
- Charlie chooses a random integer c in {1, …, r – 1}, computes cQ and sends it to Alice and Bob;
-
- Alice computes e(bP, cQ)a = e(P, Q)abc,
- Bob computes e(aP, cQ)b = e(P, Q)abc,
- Charlie computes e(aP, bQ)c = e(P, Q)abc.
- They all share the secret data e(P, Q)abc.
The security relies on the hardness of the discrete logarithm problem in the three groups G1, G2, G3 and on the hardness of inverting the pairing.
Pairings with curves over fields GF(2n) (and GF(3m)), rise and fall
(From Steven Galbraith’s talk title The fall and rise and fall and rise of supersingular elliptic curves (in cryptography)
As we have seen in the previous section, supersingular curves in small characteristic were avoided in the 90’s because of the Menezes-Okamoto-Vanstone attack.
Pairings with curves over fields Z/pZ = Fp = GF(p)
See this page Pairing-friendly curves for a short-list of interesting curves for cryptography.
Computing Discrete logarithms in Fpn = GF(pn)
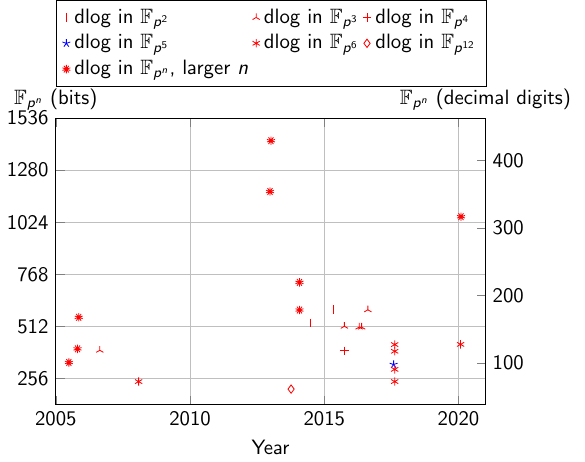
Record computations of discrete logarithms in GF(pn)
| field | bits | decimals | Date | Authors | Link | Comment |
|---|---|---|---|---|---|---|
| p2 | 595 | 29/04/2015 | Razvan Barbulescu, Pierrick Gaudry, Aurore Guillevic and François Morain | DOI | ||
| p2 | 529 | 24/06/2014 | Razvan Barbulescu, Pierrick Gaudry, Aurore Guillevic and François Morain | nmbrthy HAL | ||
| p3 | 593 | 16/08/2016 | Pierrick Gaudry, Aurore Guillevic and François Morain | nmbrthy | ||
| p3 | 508 | 23/05/2016 | Aurore Guillevic, François Morain and Emmanuel Thomé | DOI | ||
| p3 | 508 | 20/04/2016 | Aurore Guillevic and François Morain | nmbrthy | ||
| p3 | 512 | 02/10/2015 | Razvan Barbulescu, Pierrick Gaudry, Aurore Guillevic and François Morain | slides | ||
| p3 | 394 | 23/08/2006 | Antoine Joux, Reynald Lercier, Nigel Smart and Frederik Vercauteren | DOI | ||
| p4 | 392 | 02/10/2015 | Razvan Barbulescu, Pierrick Gaudry, Aurore Guillevic and François Morain | slides | ||
| p5 | 324 | 01/08/2017 | Laurent Grémy, Aurore Guillevic and François Morain | nmbrthy HAL | ||
| p6 | 423 | 29/01/2020 | Gary McGuire and Oisín Robinson | nmbrthy arxiv | ||
| p6 | 422 | 16/08/2017 | Laurent Grémy, Aurore Guillevic, François Morain and Emmanuel Thomé | DOI | ||
| p6 | 389 | 16/08/2017 | Laurent Grémy, Aurore Guillevic, François Morain and Emmanuel Thomé | DOI | Pierrick Gaudry and Marion Videau were involved in a first step of the computation (see DOI) | |
| p6 | 300 | 16/08/2017 | Laurent Grémy, Aurore Guillevic, François Morain and Emmanuel Thomé | PhD thesis | Announced in DOI, Pierrick Gaudry and Marion Videau were involved in a first step of the computation (see DOI) | |
| p6 | 240 | 16/08/2017 | Laurent Grémy, Aurore Guillevic, François Morain and Emmanuel Thomé | PhD thesis | Announced in DOI, Pierrick Gaudry and Marion Videau were involved in a first step of the computation (see DOI) | |
| p6 | 240 | 02/02/2008 | Pavol Zajac | PhD thesis | ||
| p12 | 203 | 07/10/2013 | Kenichiro Hayasaka, Kazumaro Aoki, Tetsutaro Kobayashi and Tsuyoshi Takagi | DOI DOI |
| field | bits | decimals | Date | Authors | Link | Comment |
|---|---|---|---|---|---|---|
| p50 | 1051 | 04/02/2020 | Madhurima Mukhopadhyay, Palash Sarkar, Shashank Singh and Emmanuel Thomé | ePrint | ||
| p40 | 728 | 29/01/2014 | Palash Sarkar and Shashank Singh | DOI | ||
| p37 | 592 | 29/01/2014 | Palash Sarkar and Shashank Singh | DOI | ||
| p57 | 1425 | 06/01/2013 | Antoine Joux | nmbrthy DOI | Kummer extension | |
| p47 | 1175 | 24/12/2012 | Antoine Joux | nmbrthy DOI | Kummer extension | |
| p30 | 556 | 09/11/2005 | Antoine Joux and Reynald Lercier | nmbrthy | Kummer extension | |
| p25 | 401 | 24/10/2005 | Antoine Joux and Reynald Lercier | nmbrthy DOI | ||
| p18 | 334 | 28/06/2005 | Reynald Lercier and Frederik Vercauteren | nmbrthy paper |
Choosing key-sizes
See this page Pairing-friendly curves for a short-list of interesting curves for cryptography.
How to stay up-to-date (veille technologique)
ANSSI, NIST
In France, ANSSI is in charge of recommendations web site and publishes a report named RGS (Référentiel Général de Sécurité). RGS-B1 is about cryptographic key sizes link to latest version: 2021 (previous version: 2014). In the US, for commercial and non-critical civil use, NIST (National Institute of Standards and Technology) publishes standards, organizes competitions to decide of new standards.
IACR events and publications
IACR (International Association for Cryptologic Research) conferences and workshops: all past talks are available on the Youtube channel of IACR. In particular, RWC (Real Wold Crypto) is a more applied conference, with many accessible talks (not too technical). Published papers older than two years are freely available at IACR archive.
Watch out: the online archive ePrint hosts non-reviewed draft papers. It means that in some cases, the results or the claims are wrongs (this is more a platform for hosting discussions). To ensure that the work was peer-reviewed (other specialists of the field checked the technical content) and approved, check if the paper is published at a workshop or conference. It should have a mention on the paper, usually a footnote on the first page.
Blogs
- Pr. Matthew Green blog, A few thoughts on cryptographic engineering.
- Pr. Steven Galbraith, dedicated to elliptic curves blog
- COSIC blog, research group at KU leuven, Belgium, in particular, a post on factoring
Mailing-lists
- Mailing-list
curves@moderncrypto.orgon applied cryptography related to elliptic curves. Archives at moderncrypto.org
Mathematical software
To experiment « by hand » simple cases of RSA for example, one needs a software able to handle large-precision integers. Indeed, native integers are only 64-bit long on a processor.
- SageMath is a free mathematical software whose interface has a Python-like syntax, and there is a wide free documentation, in English and in French (Zimmermann’s book).
- PARI-GP is an alternative, based on a C library, with a dedicated language (GP).
- For development, the GMP library is the reference in C language for very efficient multi-precision arithmetic.
Cours au Collège de France
With a different approach, the lectures at Collège de France are recorded and posted online. There is a department on computer science. Usually there are lectures targeting a very general audience, and also more dedicated lectures, for researchers (less accessible). About cybersecurity, there was a talk by Guillaume Poupard (head of ANSSI) in 2019: [link]https://www.college-de-france.fr/site/gerard-berry/seminar-2019-02-13-17h30.htm) (also available in audio-only format on France Culture website).
Further reading
PhD theses
Usually, PhD theses are good documents where to start reading about a new topic. Good PhD theses start with a long introduction on the topic of the thesis, assuming general knowledge (undergraduate, Master-1 level) but not dedicated knowledge of the field. To know about on-going theses in France: theses.fr. Searching PDF documents: Theses En Ligne.
Historical books
Some historical readings: big bookstores in UK even have « Bletchley Park » dedicated shelves.
Index, English-French
batch gcd: calcul de pgcd par paquets, consiste à multiplier entre eux les nombres avant de calculer des pgcd
cado-nfs: logiciel développé à Nancy pour la factorisation et le logarithme discret
DH (Diffie-Hellman): nom du cryptosystème publié en 1976
discrete logarithm: logarithme discret
finite field: corps fini
gcd (greatest common divisor): pgcd
key: clé
lsb, least significant bits: bits de poids faible
modulus: module
msb, most significant bits: bits de poids fort
number field: corps de nombres (par exemple Q(i) avec i2 = -1)
padding: remplissage
ransomware: rançongiciel
RSA (Rivest Shamir Adleman): nom du cryptosystème publié en 1977
smooth, B-smooth: friable, pour un nombre entier, se factorise en produit de nombres premiers inférieurs à une borne B
Notations
Z/nZ: the ring of integers modulo n
Z/pZ, Fp, GF(p): the prime field of p elements, where p is prime
GF(2n): the finite field of 2n elements, requires a choice of an irreducible polynomial of degree n to represent it, for example f(x) = x127 + x + 1 for n = 127



