Un château pas très fort
Les
documents disponibles sur cette page ainsi que le contenu de la page
sont mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International 
L'idée de cette activité m'est venue quand je me suis dit que, de toutes les activités que je présentais, aucune n'était vraiment proche de mes thèmes de recherche (à savoir la vérification formelle). Il y avait bien la traversée de rivière, mais elle parlait des outils de vérification, pas des méthodes. C'est donc réparé avec cette activité qui, une fois n'est pas coutume, n'est pas adaptée à un public de primaire.
Notions abordées :
Avec cette activité, tout en jouant dans un château fort, on entre vraiment dans les mécanismes de vérification formelle de systèmes informatiques. On apprend à écrire une formule logique pour décrire précisément une propriété, puis on voit comment l'ordinateur vérifie si un système la satisfait. On utilise au passage les opérateurs logiques classiques (ET, OU, NON, implication).
Public :
Cette activité a été testée devant un public adulte non scientifique, et avec des élèves de 1ère scientifique. Elle ne me semble pas adaptée avant la toute fin de collège, voire lycée.
J'ai été surprise de voir la réactivité et la vivacité d'élèves de première scientifique face à cette activité. C'est tout de même une partie de mon cours de Master !! Elle nécessite de comprendre et d'utiliser un nouveau langage appelé "logique", puis de réfléchir ensemble à un algorithme sur le graphe représentant le château.
Matériel :
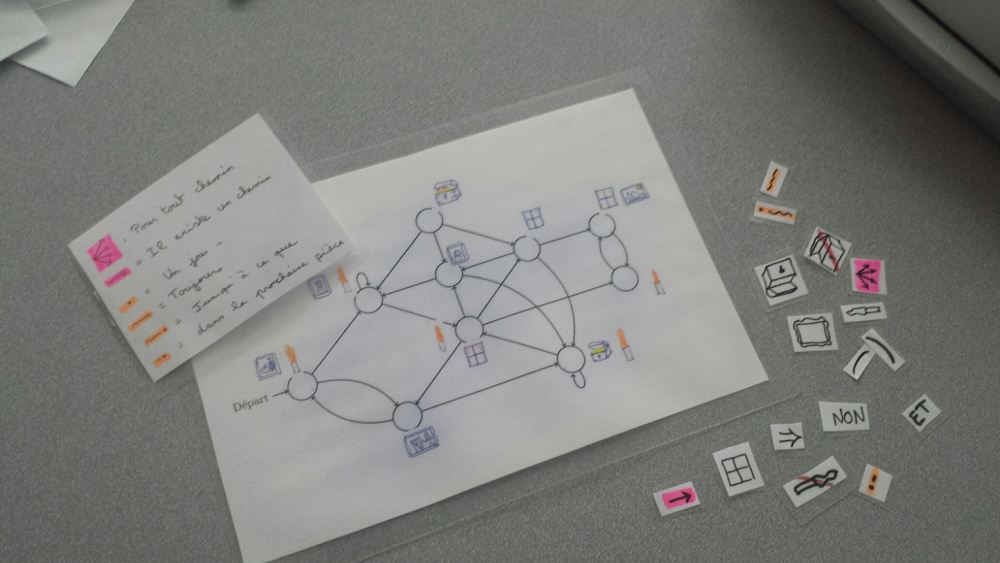 Voir la section lien pour des exemples à imprimer ou
à refaire en plus beau.
Voir la section lien pour des exemples à imprimer ou
à refaire en plus beau.
- le plan du château, plastifié, imprimé sur une feuille A4,
- les opérateurs logiques, découpés puis plastifiés (pour prolonger leur durée de vie).
- Un aide mémoire pour se souvenir de ce que signifient les opérateurs "nouveaux", c'est à dire ceux autres que les classiques ET, OU, l'implication et NON.
Principe :
Cette activité illustre une méthode de vérification formelle de systèmes informatiques appelée model-checking (et donc littéralement vérification de modèles). Le principe est de représenter son système (ici le château) par un modèle (ici un automate), qui a l'avantage d'avoir une définition très précise. En clair quand on regarde l'automate du château on sait précisément tous les passages (les flèches, ou transitions) qui existent entre deux pièces (les cercles, appelés états).
De même on va représenter les propriétés qui nous intéressent (comme par exemple l'existence d'un chemin qui va passer dans une salle ayant à la fois une torche et un tableau) de manière formelle, dans un langage logique. Pour cela on va utiliser des opérateurs et les assembler, un peu comme on peut combiner des mots pour apprendre à faire des phrases en CP (c'est d'ailleurs la présence d'une de mes filles en CP qui m'a donné l'idée).
Une fois cela fait il existe des logiciels qui permettent de vérifier automatiquement si le modèle du sytème satisfait la propriété, et on va voir comment ils fonctionnent.
- On va d'abord commencer par découvrir les opérateurs, leur signification et comment les combiner en écrivant des propriétés du genre Je peux aller jusqu'à une fenêtre ou bien Je vais forcément passer devant un tableau.
- On peut ensuite compliquer les propriétés, pour exprimer que quelqu'un qui a peur du noir peut atteindre un trésor ou encore que on peut se perdre dans le chateau et arriver dans une pièce à partir de laquelle il est impossible d'accéder au trésor
- En faisant cela on va voir à la main si ces propriétés sont satisfaites sur le modèle. Cela consiste à voir si l'on trouve le chemin demandé ou si l'on peut s'assurer (et convaincre les autres) qu'il n'existe pas.
- Seulement le faire avec les mains et juste son pouvoir de conviction, c'est parfois un peu limité. Et comment ferait-on si le système était plus gros, ou si l'on voulait trouver tous les états qui satisfont une formule (et pas juste vérifier si l'état de départ la satisfait) ? On s'intéresse donc aux algorithmes qui permettent de vérifier cela automatiquement, et en partant d'une formule simple, par exemple Il existe un chemin un jour fenêtre on peut retrouver cet algorithme, et déterminer en raisonnant de proche en proche tous les états qui satisfont cette propriété. On utilise pour cela ce qu'on appelle un algorithme de point fixe.
Extensions :
Vous êtes bien entendu encouragés, une fois le principe compris, à créer vos propres systèmes, soit fictifs comme celui-ci soit inspirés de systèmes réels.
Liens :
- La vidéo de présentation est disponible sur Youtube.
Nouveautés août 2017 :
- Vous pouvez télécharger la version remasterisée (en LaTeX avec TikZ pour ceux à qui ça parle) du plan du château et des opérateurs logiques.
- une fiche complète pour expliquer l'activité.
Photos :
Voici à quoi ressemblaient, avant le passage à une
version dessinée par ordinateur, l'activité
en conditions réelles et le matériel.


