Curved Kernel

Our overall goal is to extend to curved objects the definitions of the classical geometric structures and the algorithms to compute them.

The goal is also implementation in the CGAL Library. Historically, the CGAL kernels provided the user mainly with linear objects (points, line segments, lines...) and predicates on them. Curves were present in the traits classes of certain specific packages: arrangement with a traits class for conic arcs, optimization with conics, Apollonius graph with circles. There is a need for a general kernel providing the user with - classes for curved objects - predicates and constructions on them. The effort consists first of all on defining general concepts. On the implementation side, a kernel for 2D circular arcs was first released in CGAL 3.2 and a kernel for 3D circular arcs was released in CGAL 3.4. The curved kernel is parameterized by a BasicKernel parameter and derives from it, in order to include all needed functionality on basic geometric objects, like points, line segments, and so on. The curved kernel is also parameterized by an AlgebraicKernel that is responsible for all algebraic computations. The declaration is the following:   template < typename BasicKernel, typename AlgebraicKernel >   class Curved_kernel;

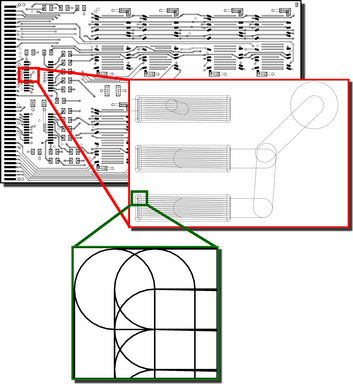
Arrangement computed with the CGAL Circular kernel and Arrangement packages, on industrial VLSI data. The zooms show the complexity of the data. (Thanks to GeometryFactory for the data and to Pierre Alliez for the picture)

The algebraic kernel consists in fact of several concepts, such as:
  - univariate and bivariate polynomials,
  - algebraic numbers, ie roots of univariate polynomials,
  - roots of systems of bivariate polynomials.
The basic operations necessary to implement geometric predicates and constructions should not impose any specific algebraic tool, so they are kept at a high level, like:

	. compare on algebraic numbers and roots of polynomial systems,   . solve on systems of bivariate polynomials,   . critical_points on bivariate polynomials,   . sign_at that computes the sign of a bivariate polynomial evaluated at roots of polynomial systems.

It is crucial to note that the concepts must be general enough to allow also completely different methods, such as interval analysis, that will be used together with exact algebraic methods, for filtering purposes.

Concepts for univariate and bivariate polynomials were reviewed and accepted by the CGAL editorial board.
Models for univariate polynomials, based on the RS software package, should be released soon in CGAL 3.6.
Other models, for both univariate and bivariate polynomials, are expected in the future.

CGAL Packages
2D Circular kernel
3D Spherical kernel
Algebraic Kernel specifications, in collaboration with Eric Berberich and Michael Hemmer

Contributors
Eric Berberich
Pedro M. M. de Castro (internship, summer 2006, now PhD student)
Frédric Cazals
Ioannis Z. Emiris
Julien Hazebrouk and Damien Leroy (project, winter 2006)
Michael Hemmer
Athanasios V. Kakargias (internship, summer 2003)
Menelaos Karavelas
Sylvain Lazard
Sébastien Loriot
Luis Peñaranda
Sylvain Pion
Ilya Suslov (internship, winter 2006)
Elias Tsigaridas
Constantinos Tsirogiannis and Julien Hazebrouk (internships, summer 2005)

Papers

• Towards an Open Curved Kernel (Symposium on Computational Geometry, 2004)
  by Ioannis Z. Emiris, Athanasios Kakargias, Sylvain Pion, Monique Teillaud and Elias P. Tsigaridas.
• Exact and efficient computations on circles in CGAL and applications to VLSI design (EuroCG'07)
  by Pedro Machado Manhães de Castro, Sylvain Pion and Monique Teillaud.
• Design of the CGAL 3D Spherical Kernel and application to arrangements of circles on a sphere (Computational Geometry: Theory and Applications, 2009)
  by Pedro Machado Manhães de Castro, Frédéric Cazals, Sébastien Loriot, Monique Teillaud.

Slides
Introduction to CGAL
Introduction to the curved kernel (Arcadia meeting, 2005)
CGAL news (Dagstuhl Seminar, 2005)
From triangles to curves (invited talk - European Workshop on Computational Geometry, Delphi, March 27-29, 2006)
Design of the CGAL 3D Spherical Kernel (Dagstuhl Seminar, 2007)
Design of the Spherical Kernel (Workshop WRSO, 2007)

Research reports

ECG First Prototype of a CGAL Geometric Kernel with Circular Arcs Methods to compare real roots of polynomials of small degree Towards a CGAL-like kernel for curves Comparison of fourth-degree algebraic numbers and applications to geometric predicates

ACS Geometric filtering of primitives on circular arcs (2006) Prototype implementation of the algebraic kernel (2006) Interface specification of algebraic kernel (2006) On the evaluation of 2D curved kernels (2006) Benchmarking of different arrangement traits (2006) CGAL package for 2D curved kernel (2006) Revision of Interface specification of algebraic kernel (2007) Benchmarks and evaluation of algebraic kernels for circles (2007) CGAL package for 2d filtered circular kernel (2007) Specifications of the CGAL 3D Circular Kernel (2007) CGAL 3D Spherical Kernel (2008)

This work was partially supported by the IST Programme of the 6th Framework Programme of the EU as a STREP (FET Open Scheme) Project under Contract No IST-006413 (ACS - Algorithms for Complex Shapes) This work was partially supported by the IST Programme of the EU as a Shared-cost RTD (FET Open) Project under Contract No IST-2000-26473 (ECG - Effective Computational Geometry for Curves and Surfaces) Preliminary work was done partially within the INRIA Associate Team CALAMATA.