Algorithmique - TP2

1 Intégrales

1.1 Première partie

Dans cette première partie, on cherche à donner une valeur approchée de l’intégrale de la fonction \(\frac{1}{1+x}\) entre 0 et 1, c’est à dire une valeur approchée de \(\ln 2\).

Plus généralement, on cherche à donner une valeur approchée de \(\int_0^1 f(x) dx\).

L’idée est la suivante: L’intégrale de la fonction \(f\) peut se comprendre comme l’aire sous la courbe de \(f\):

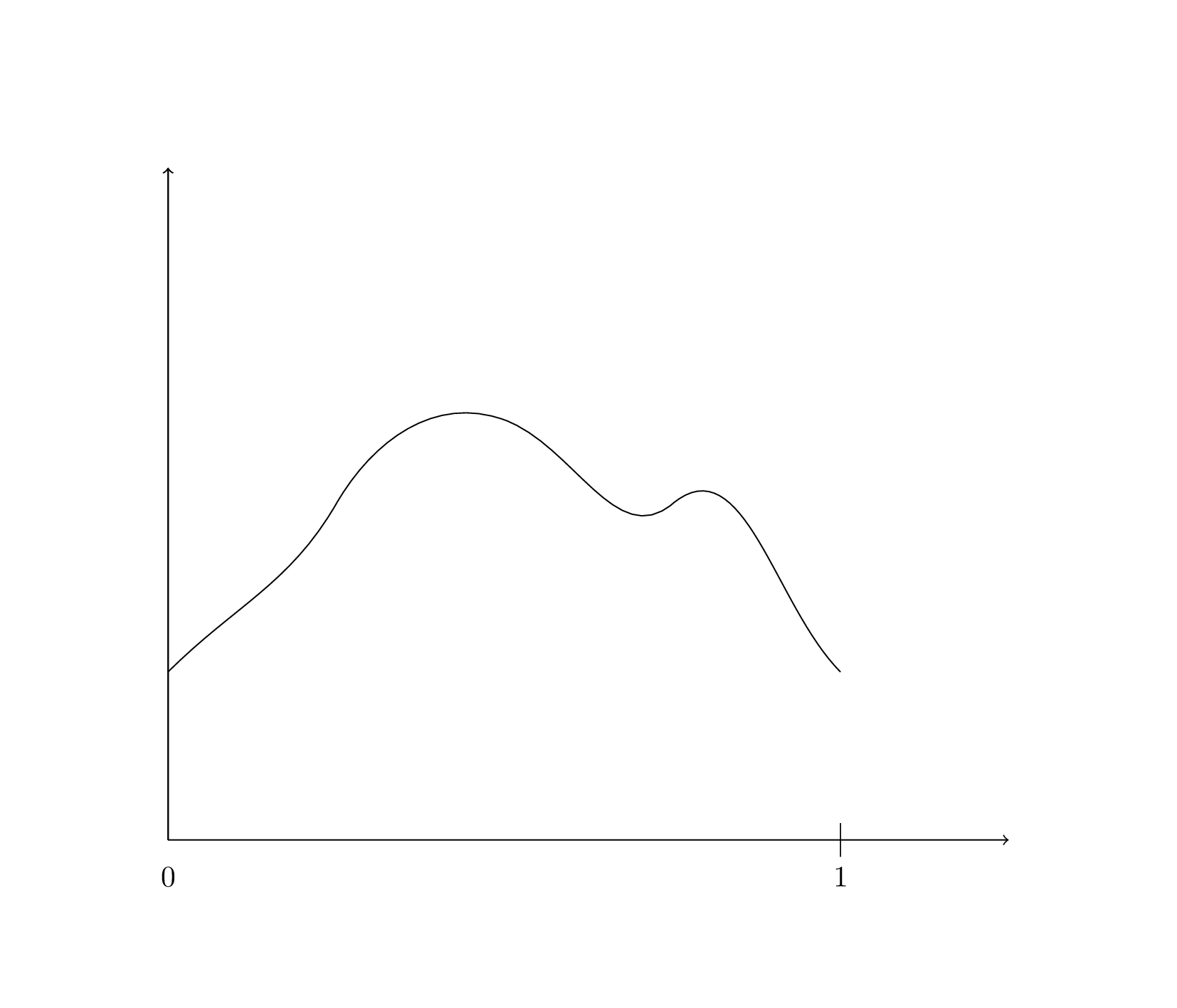
Pour calculer cette aire, on choisit un entier \(n\) et on divise l’intervalle \([0,1]\) en \(n\) intervalles égaux \([x_0, x_1], [x_1, x_2] \dots [x_{n-1}, x_n]\). On a donc \(x_i = i / n\).

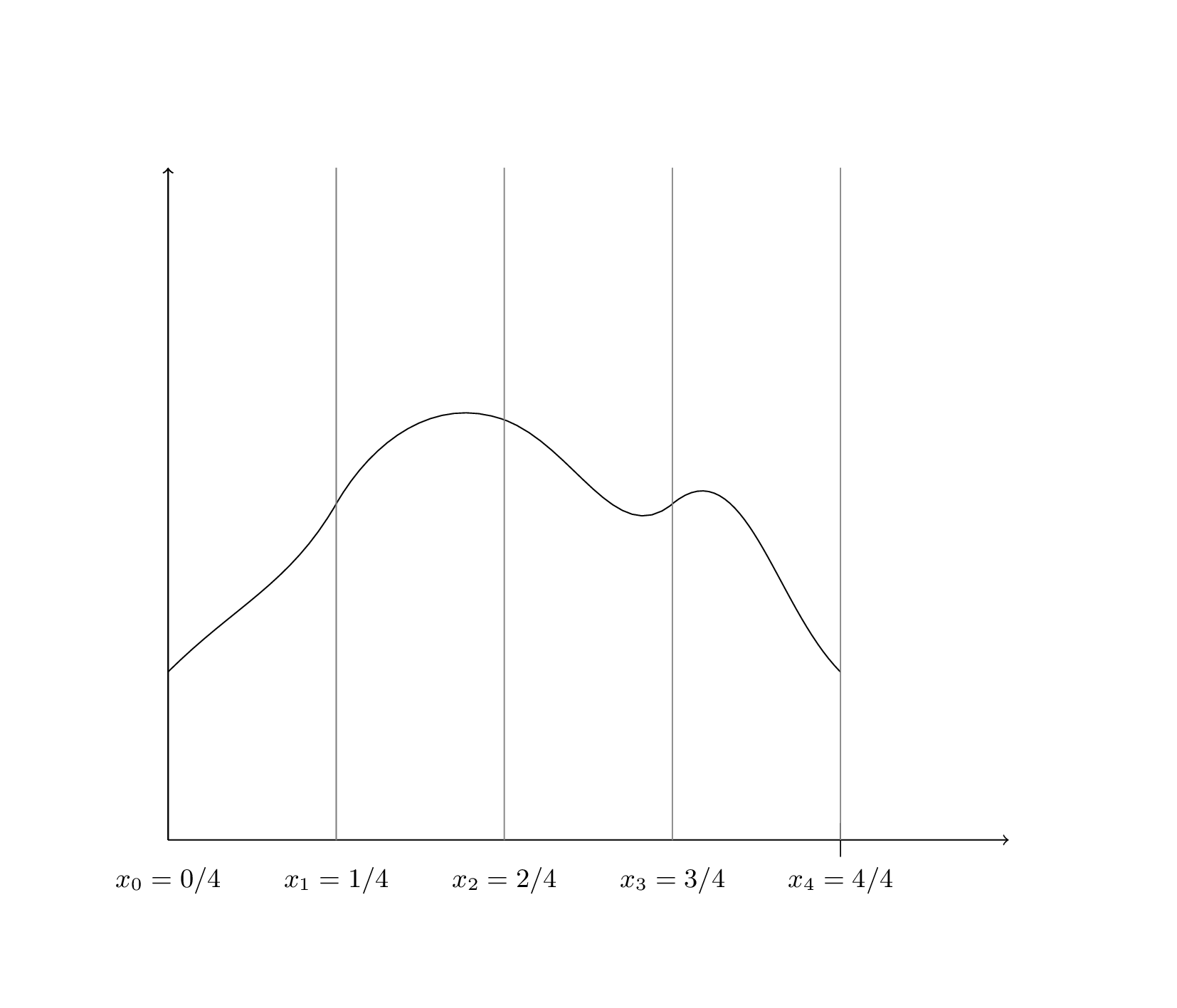
La première méthode pour approcher l’aire est de calculer, dans chaque intervalle \([x_i, x_{i+1}]\), l’aire du rectangle “de gauche”, c’est à dire dont la hauteur est égal à \(f(x_i)\), et on ajoute ensuite toutes ces aires.

Le tout premier rectangle par exemple est de hauteur \(f(x_0) = f(0)\) et de longueur \(1/n\), sa surface est donc \(f(0)/n\).

• Ecrire une fonction python integrale_gauche(n) qui divise l’intervalle \([0,1]\) en \(n\)-sous intervalles et qui calcule une valeur approchée de l’intégrale de \(f(x) = 1/(1+x)\) en utilisant la méthode ci-dessus. Tester pour \(n = 4\) (on devrait trouver approximativement \(0.75952\)) et \(n = 1000\).

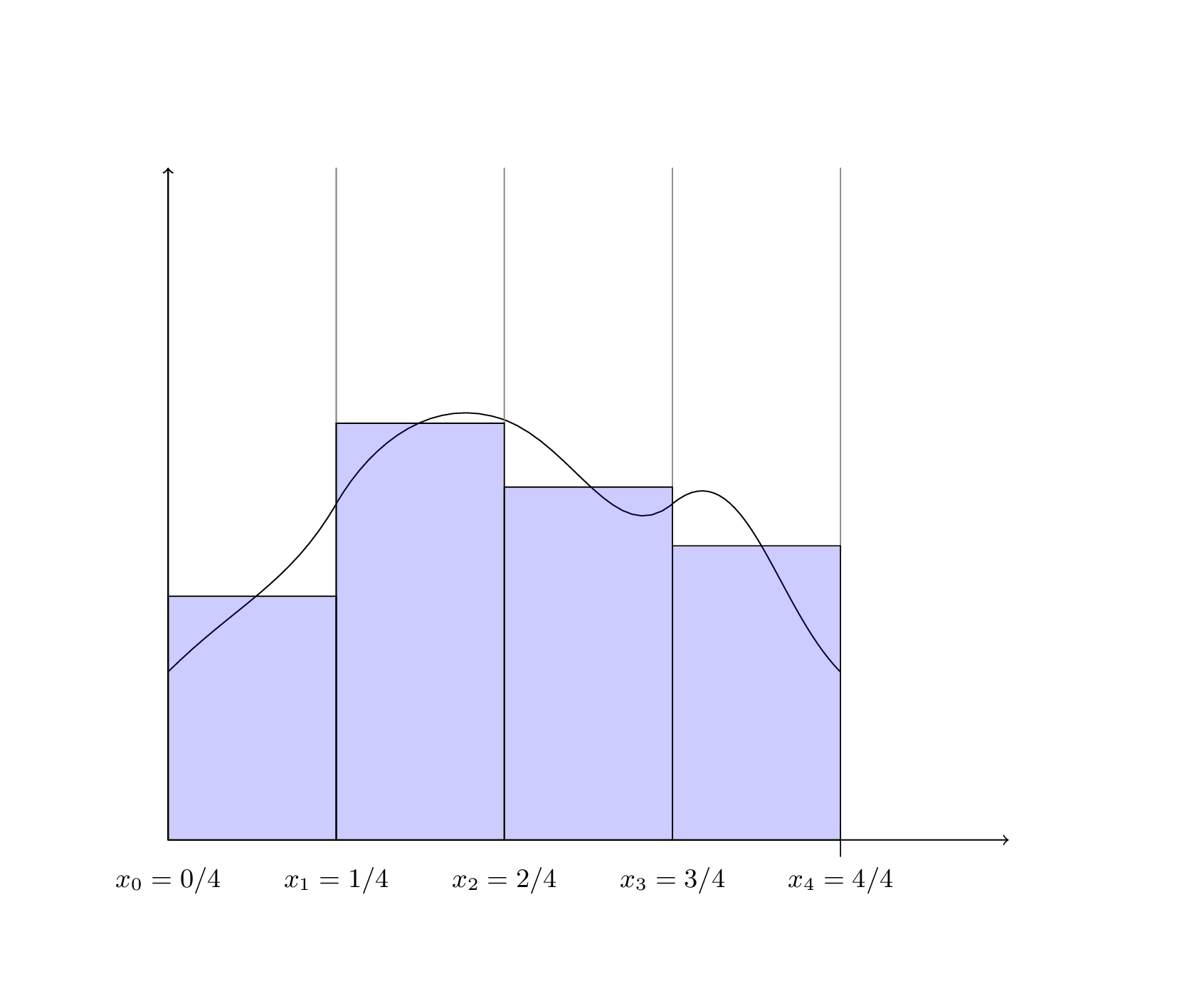
Une deuxième méthode fait pareil, mais avec l’aire du rectangle “de droite”: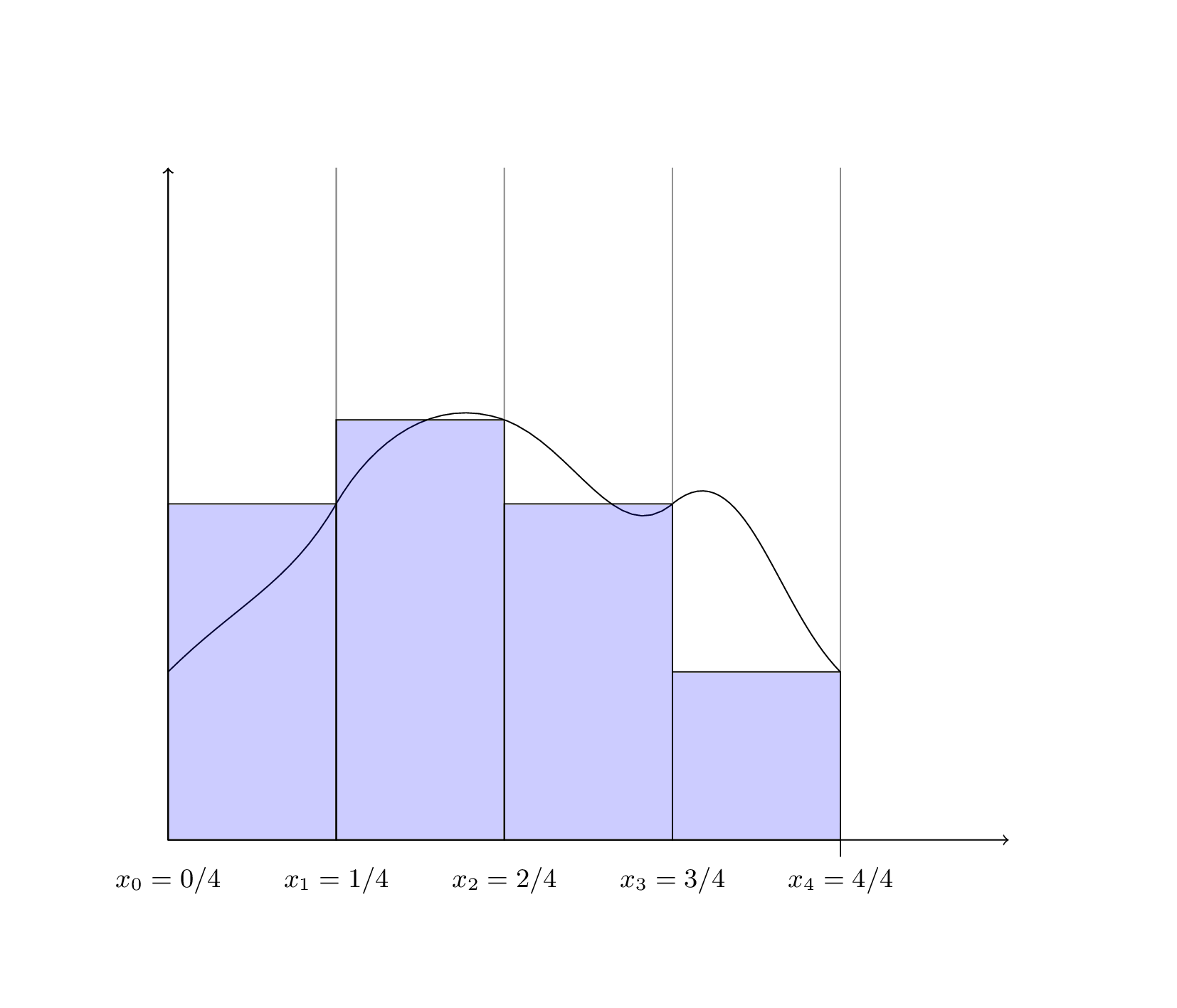

• Ecrire une fonction python integrale_droite(n) qui divise l’intervalle \([0,1]\) en \(n\)-sous intervalles et qui calcule une valeur approchée de l’intégrale de \(f(x) = 1/(1+x)\) en utilisant la méthode ci-dessus.

Une troisième méthode consiste à utiliser comme hauteur la valeur \(f(y)\) où \(y\) est le point au milieu du segment \([x_i, x_{i+1}]\):

• Ecrire une fonction python integrale_milieu(n) qui divise l’intervalle \([0,1]\) en \(n\)-sous intervalles et qui calcule une valeur approchée de l’intégrale de \(f(x) = 1/(1+x)\) en utilisant la méthode ci-dessus. Pour \(n = 4\), on devrait trouver approximativement \(0.6912\).

Une dernière méthode est de calculer l’aire du trapèze qui s’appuie sur \(f(x_i)\) et \(f(x_{i+1})\):

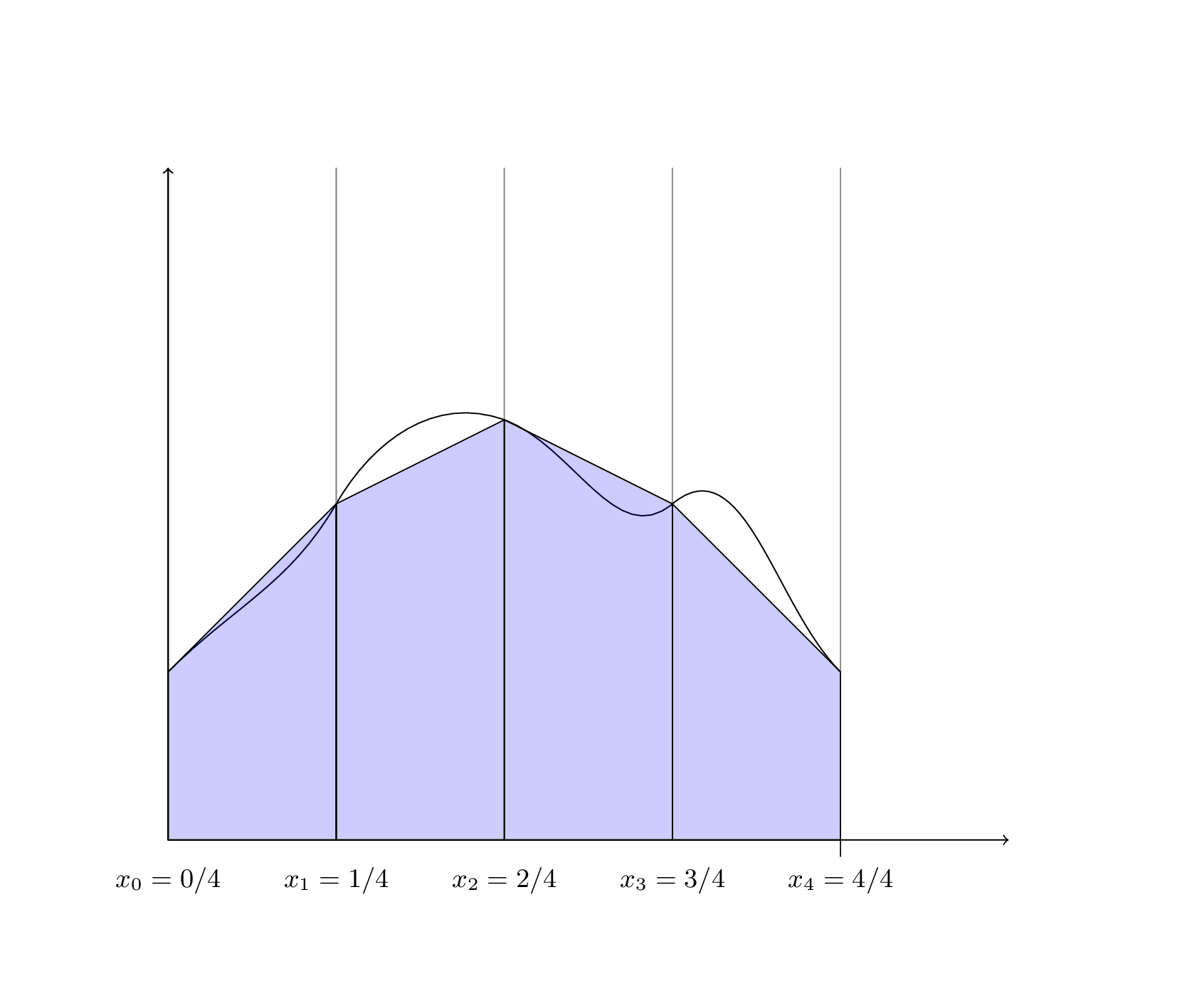
On rappelle que l’aire d’un trapèze s’obtient par la formule \(\frac{(base1 + base2) \times (hauteur)}{2}\)

• Ecrire une fonction python integrale_trapeze(n) qui divise l’intervalle \([0,1]\) en \(n\)-sous intervalles et qui calcule une valeur approchée de l’intégrale de \(f(x) = 1/(1+x)\) en utilisant la méthode ci-dessus. Pour \(n = 4\), on devrait trouver approximativement \(0.6970\).

• Dans un fichier texte, ou dans une feuille de calcul Libreoffice, notez les valeurs approchées pour \(\ln 2\) obtenues avec les \(4\) méthodes pour \(n = 4\) et \(n = 1000\), et comparez-les avec la vraie valeur de \(\ln 2\). Quelle est la méthode qui donne le plus de chiffres précis de \(\ln 2\) ? On peut obtenir la valeur de \(\ln 2\) avec le programme suivant:

import math
print(math.log(2))

1.2 Deuxième partie

En python, une fonction peut prendre en argument une autre fonction:

def test(f,n):
    return f(n) + f(n+1)


def g(x):
    return x**2 - 3*x + 1

# calcule g(4) + g(5)
print(test(g, 4))

• Modifier les 4 fonctions précédentes pour qu’elles prennent en argument la fonction \(f\) dont on veut calculer l’intégrale sur \([0,1]\). Vérifiez que tout fonctionne correctement en testant avec la fonction suivante:

def f1(x):
    return 1/(x+1)

• Tester les 4 manières de calculer une intégrale pour la fonction suivante, avec \(n = 4\) et \(n= 1000\), et déterminez la méthode qui donne le plus de chiffres précis de \(\pi\).

def f2(x):
    return 4/(x*x+1)

1.3 Troisième partie

• Modifiez les fonctions pour qu’elles fonctionnent sur n’importe quel intervalle \([a,b]\). Elles prendront donc 4 arguments: \(f,a,b,n\).

Attention, la formule pour calculer les \(x_i\) n’est plus la même. Essayez de la trouver tout-e seul-e avec un papier et un crayon. Si vous n’y arrivez pas, cliquez sur la solution¹.

• Vérifiez que tout fonctionne en calculant l’intégrale de \(10\) à \(20\) de la fonction \(1/x\) (ça fait encore \(\ln 2\)).

1.4 Quatrième partie

On suppose maintenant que la fonction \(f\) qu’on veut intégrer est décroissante sur l’intervalle \([a,b]\). Dans ce cas, integrale_gauche(f,a,b,n) donne une valeur trop élevée de l’intégrale, et integrale_droite(f,a,b,n) donne une valeur trop petite de l’intégrale.

• Ecrire une fonction integrale(f,a,b, epsilon) qui calcule une valeur de l’intégrale de \(f\) sur l’intervalle \([a,b]\) avec une précision \(\epsilon\). Pour cela:

  • On commence avec \(n = 2\).
  • On calcule l’intégrale gauche et l’intégrale droite. Si la différence entre les deux est inférieure à \(\epsilon\), on renvoie la valeur d’une des deux intégrales. Sinon, on multiplie \(n\) par \(2\) et on recommence.

• Donner une approximation de \(\ln 2\) et de \(\pi\) à \(0.00001\) près en utilisant cette fonction.

2 Suite

• Reprenez le TP précédent.

Notes de bas de page

1. \(x_i = a + i \frac{(b-a)}{n}\)