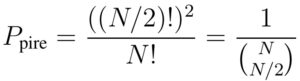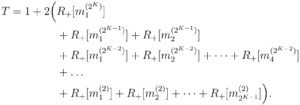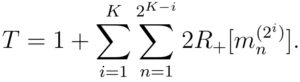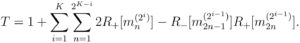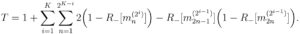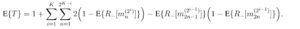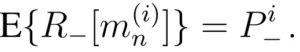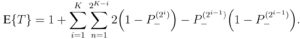Update 17/12/2020 : Depuis la création de ce billet, un groupe de chercheur français a créé un site web regroupant les publications et articles de presse récents sur l’utilisation des tests groupés pour le dépistage du COVID-19 dans le monde. Allez-y faire un tour! https://www.groupool-covid19.org/
Alors que la majorité de la population mondiale est désormais confinée pour lutter contre la propagation du nouveau coronavirus, il se pose la question de l’après. Une fois que les mesures de confinement seront progressivement levées, la clé pour éviter des deuxièmes et troisièmes vagues de la pandémie sera un dépistage massif et rapide, combiné avec un suivi des cas et des quarantaines ciblées. Hélas, la capacité de test de la plupart des pays est à l’heure actuelle loin d’être suffisante.
La semaine dernière, des chercheurs du service de don de sang de la croix rouge de Francfort et de l’institut de virologie médicale de l’hôpital universitaire de Francfort et de l’université Goethe ont réussi à développer une procédure qui rend possible une augmentation drastique et immédiate des capacités de dépistage mondiales pour le SARS-CoV-2, le virus derrière la maladie COVID-19. La procédure se base sur le test groupé (group testing), un principe aussi simple que génial, qui était déjà utilisé pour le dépistage de la syphilis pendant la deuxième guerre mondiale. Au lieu d’analyser individuellement les échantillons des patients (généralement des prélèvements muqueux du nez ou de la gorge), on en mélange plusieurs ensemble, disons 8, puis on effectue un test sur ce cocktail, appelé mini-groupe. Si le résultat est négatif, on peut conclure de façon fiable qu’aucun des 8 patients n’est infecté, en un seul test ! Si le test est positif, on divise les échantillons en deux groupes de 4 puis on répète la procédure, jusqu’à ce qu’un test négatif soit obtenu ou qu’un seul échantillon ne reste.
Cette procédure pourrait d’ors et déjà être mise en oeuvre dans n’importe quel laboratoire du monde, sans besoin d’équipement supplémentaire. Etant donné qu’un seul test PCR pour le COVID-19 peut prendre plusieurs heures sur une machine dédiée, diviser leur nombre pourrait faire gagner un temps précieux dans la lutte contre SARS-CoV-2.
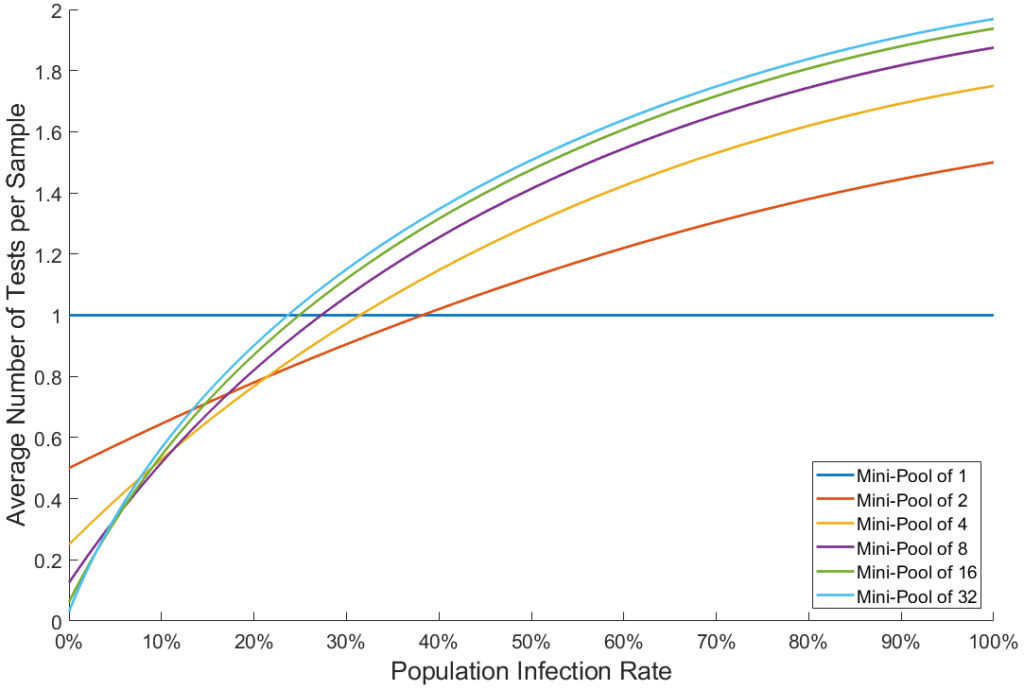
Mais combien de temps exactement ? Le graphique ci-dessous montre le nombre théorique moyen de tests par échantillon requis un utilisant le test groupé, en fonction du taux d’infection de la population, pour différentes tailles de mini-groupes (mini-pool):
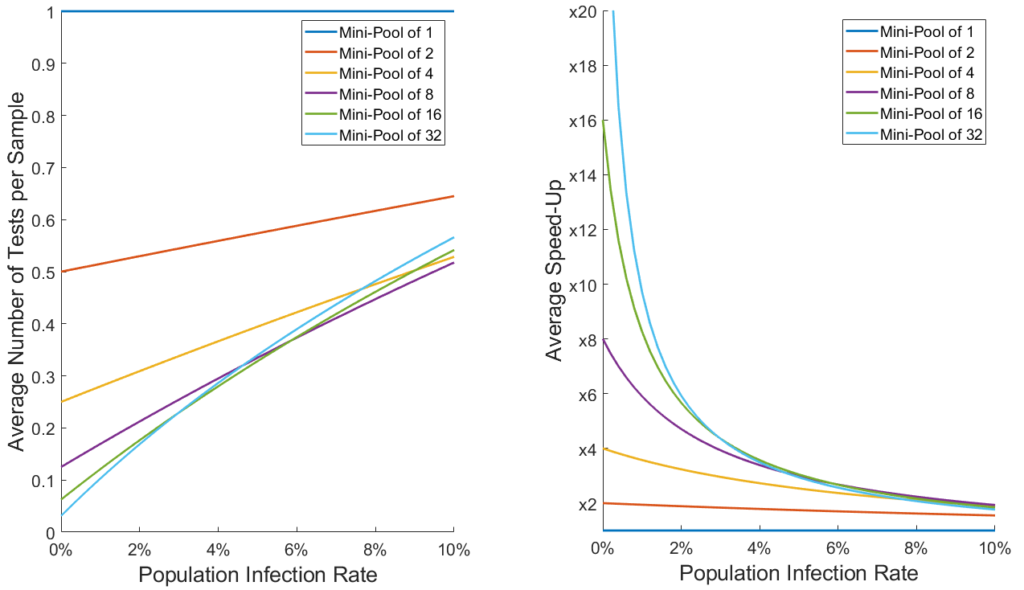
Notons qu’utiliser des mini-groupes de taille 1 correspond au dépistage classique: un test par échantillon. Le graphique montre que si la proportion de personnes infectées au sein de la population est supérieure à 25%, le test groupé n’est pas avantageux par rapport au dépistage conventionnel. Cependant, dans un scénario ou de grandes campagnes de tests seront conduites sur des gens pris au hasard dans les villes de façon à isoler les cas positifs au COVID-19, il est raisonnable de supposer que moins de 10% de la population sera infectée à un instant donné. Voici une version zoomée du graphique précédent, pour des taux d’infections en dessous de 10%. On montre également à droite l’inverse du graphique, correspondant au gain de vitesse moyen apporté par le test groupé:
On peut voir que pour des taux d’infection autour de 5%, utiliser des mini-groupes de 4 augmente déjà la capacité de test d’un facteur 2,5, alors que pour des taux autour de 1%, des mini-groupes de 16 pourrait multiplier par 10 la vitesse des tests ! Il est aussi intéressant de noter que pour des taux d’infection au dessus d’environ 6%, utiliser des mini-groupes supérieure à 4 n’améliore pas significativement les résultats.
Obtenir les formules correspondant à ces graphiques est en fait un problème de maths assez amusant. Dans le reste de ce billet, j’essairai d’expliquer comment le faire de façon accessible. Mon but est de partager des maths à la fois fun et utile pour s’occuper pendant le confinement ! J’espère aussi secrètement que cela pourra aider à sensibiliser aux tests groupés sur le COVID-19, qui n’ont pas l’air d’avoir reçu beaucoup d’attention par les médias ou les politiciens jusqu’ici. Faisons passer le message !
1. Hypothèses
Premièrement, nous allons supposer que chaque test peut détecter un échantillon positif dans un mini-groupe avec 100% de précision (pas de faux-positifs ni de faux-négatifs). L’étude allemande sur le SARS-CoV-2 évoquée plus haut montre qu’il est possible d’utiliser des mini-groupes de 5 échantillons sans affecter la précision des tests. Ce papier récent de l’Institut Israélien de Technologie et du Campus Rambam pour la Santé (Haifa, Israel) suggère que des groupes contenant jusqu’à 32 ou même 64 échantillons pourraient être utilisés tout en gardant le taux de faux-négatifs relativement bas. Des cycles d’amplifications (conduire plusieurs tests) peuvent aussi être utilisés pour améliorer la fiabilité, mais nous n’étudierons pas ça ici.
Deuxièmement, nous supposerons que tous les échantillons ont la même probabilité indépendante P+ (entre 0 et 1) d’être positif, représentant le taux d’infection de la population étudiée. Notons que cette hypothèse d’indépendance n’est pas valide si l’on test, par exemple, un groupe de personne vivant dans le même logement. Ici, nous supposons que les échantillons sont pris aléatoirement et uniformément au sein d’une population infectée.
Enfin, pour la clarté de l’exposé, nous ne considèreront que des mini-groupes dont la taille N est une puissance de 2, par exemple, 23 = 2 x 2 x 2 = 8. Cela rend les claculs plus faciles et plus propres.
2. Pire cas pour le nombre de tests
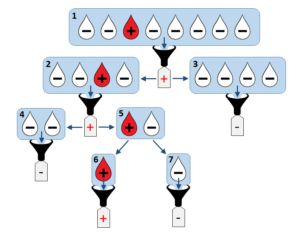
Commençons par un exercice d’échauffement: Quel est le nombre maximum Tmax de tests nécessaires pour analyser un mini-groupe de N=2K échantillons ? Ceci correspond au « pire cas » où tous les mini-groupes sont testés positifs au long de la procédure, et doivent donc être divisés en deux sous groupes pour continuer l’analyse. Un exemple d’une telle situation est illustré ci-dessous:
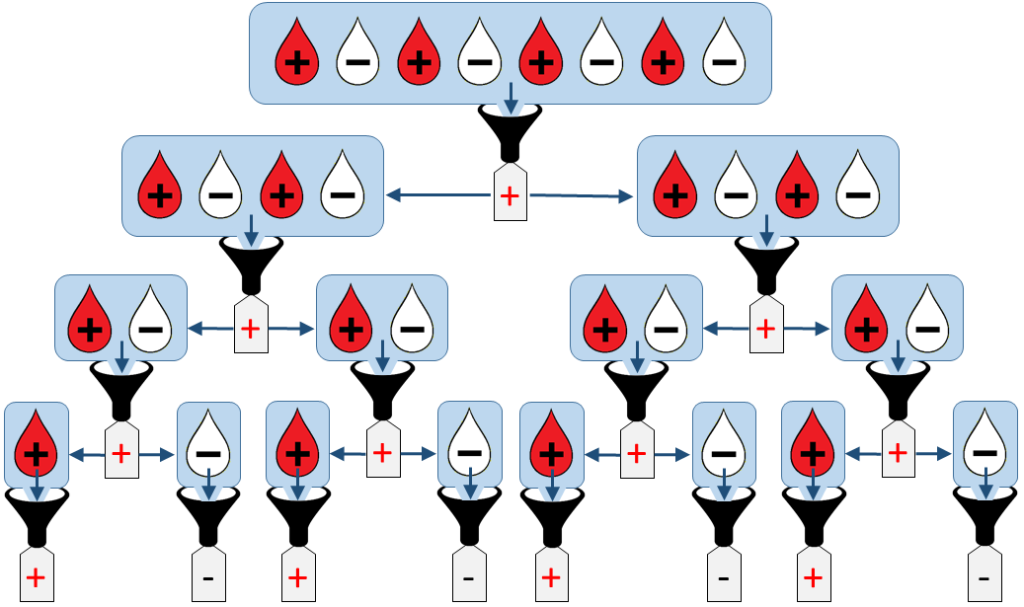
En comptant le nombre de mini-groupes de taille >1, nous voyons que:
En utilisant la formule pour les sommes de séries géométriques, nous obtenons:
Mince! Dans le pire des cas, nous voyons qu’il faut donc conduire plus de tests qu’en testant chaque échantillon un par un. Le test groupé est-il vraiment si efficace, finalement ?
Et bien, tout dépend de la fréquence à laquelle ce pire cas peut se produire. Pour en avoir une idée, restons sur l’exemple de la Figure 2 où exactement la moitié des échantillons à tester sont positifs. Dans cette situation, le pire cas ne se produit que si les échantillons sont précisément dans l’ordre alterné +,–,+,–,… La probabilité que ça arrive est le nombre d’arrangements alternés divisé par le nombre total d’arrangements:
Pour ordonner N échantillons, il y’a N façons de choisir le premier, puis (N-1) façons de choisir le deuxième, (N-2) façons de choisir le troisième, etc. Le nombre total d’arrangements est donc N x (N-1) x (N-2) x … x 1 = N! (« N factoriel »). Pour les arranger en alternance, il y a (N/2)! façons d’arranger les échantillons positifs, et (N/2)! façon d’arranger les échantillons négatifs, soit (N/2)! x (N/2)! = ((N/2)!)² façons en tout. On obtient donc:
où nous avons utilisé la notation combinatoire suivante:
prononcée « k parmi n ». Cette quantité compte le nombre de façons de placer k éléments identiques dans n emplacements. Voici un résumé de nos résultats pour différentes valeurs de N:
| Taille du mini-groupe initial N | Nombre maximum de tests Tmax | Probabilité Ppire (pour la moitié d’infectés) |
| 2 | 3 | 1/2 |
| 4 | 7 | 1/6 |
| 8 | 15 | 1/70 |
| 16 | 31 | 1/12,870 |
| 32 | 63 | 1/601,080,390 |
Comme on peut le voir, le pire cas n’arrive que très rarement lorsqu’on utilise des mini-groupes suffisamment larges. C’est rassurant !
3. Nombre moyen de tests
Intéressons-nous maintenant au problème plus général du nombre moyen de tests nécessaire pour un mini-groupe initial de taille N, et un taux d’infection P+. Pour aborder cette question, nous allons devoir introduire quelques notations utiles (c’est souvent la partie la plus difficile d’un problème de maths !). Nous désignerons par m(i) un mini-groupe de i échantillons. Les mini-groupes d’une taille donnée seront numérotés « de gauche à droite », comme indiqué dans l’exemple ci-dessous:
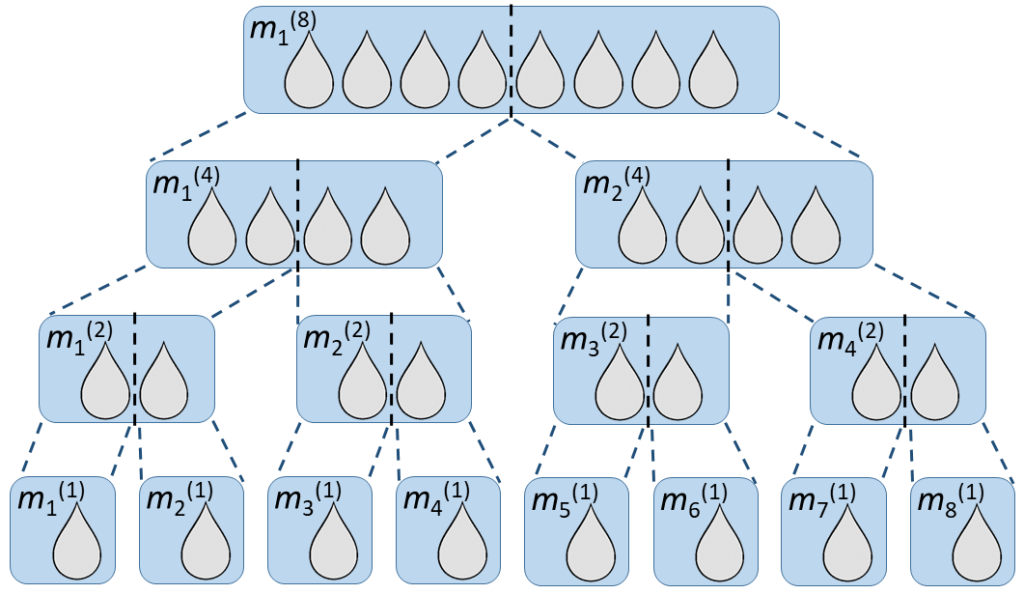
Avec cette notation, les échantillons individuels sont donc désignés commes des « groupes de 1 », c’est à dire, m1(1), m2(1), … , mN(1). Nous désignerons par R+[m(i)] la positivité d’un mini-groupe, où R+[m(i)]=1 si m(i) contient un échantillon positif et R+[m(i)]=0 sinon. De la même manière, nous appellerons R–[m(i)] = ( 1 – R+[m(i)] ) la négativité d’un mini-groupe.
Pour effectuer un test groupé, nous devons d’abord tester le mini-groupe initial, contenant tous les échantillons. Ensuite, à chaque fois qu’un mini-groupe est testé positif, nous le divisons en 2 sous-groupes de même taille et conduisons des tests supplémentaires sur chacun d’eux. Une première approche pour estimer le nombre de tests nécessaires est donc de compter deux fois le nombre de mini-groupes positifs de taille 2 ou plus. En utilisant nos notations, cela donne:
Ceci peut être écrit de façon plus compact en utilisant le symbole mathématique pour les sommes:
Cependant, cette formule oublie les « racourcis », comme celui montré dans la Figure 1. Lorsqu’un mini-groupe est testé positivement, si la première moitié de ce groupe est testé négativement, nous pouvons en déduire que la deuxième moitié est positive, sans avoir besoin de la tester. Pour enlever ces racourcis de notre comptage, il faut corriger la formule ci-dessus comme suit:
Ce nouveau terme enlève 1 à chaque fois que la première moitié d’un mini-groupe est négative alors que sa deuxième moitié est positive. Pour ce qui suit, il sera plus pratique de réécrire cette formule uniquement en fonction de la négativité des mini-groupes, comme ceci:
Nous voulons maintenant savoir quelle sera la valeur de T en moyenne, sachant que chaque échantillon individuel a une probabilité P+ d’être positif. Cette quantité moyenne est appelée « espérance de T » et nous la noterons E{T}. En utilisant le fait que l’espérance est linéaire et que l’espérance du produit de deux variables indépendantes est le produit de leurs espérances, on déduit de la formule précédente:
Il ne nous reste donc plus qu’à calculer les espérances des négativités des mini-groupes. D’après notre hypothèse, un échantillon seul est négatif avec une probabilité P–=(1-P+) (le taux de non-infection). Nous avons donc:
pour tout n entre 1 et N. De plus, un mélange de i échantillons sera testé négatif si et seulement si tous les échantillons qui le composent sont négatifs. L’espérance de sa négativité est donc le produit des espérances de ses échantillons, soit (P– ) x (P– ) x (P– ) x … Cela donne:
En insérant le tout dans l’expression précédente de E{T}, on obtient:
Après simplification, on arrive enfin à la formule générale calculant le nombre moyen de tests en fonction de la taille du mini-groupe et du taux de non-infection:
Il est également utile d’exprimer le nombre moyen de tests par échantillon. Pour cela, il suffit de diviser l’expression ci-dessus par la taille du mini-groupe initial, N=2K :
Cette expression est un polynôme en P–. Comme attendu, nous constatons que si la population est infectée à 100% (P– = 0), le test groupé requiert environ deux fois plus de tests qu’une procédure classique (c’est le « pire cas » étudié dans la section précédente). Nous voyons aussi que le nombre de tests requis décroit avec le taux d’infection, comme montré dans les graphiques en haut de ce billet.
Voici un tableau détaillant quelques valeurs approchées du nombre moyen de tests par échantillon nécessaire en fonction du taux d’infection et de la taille du mini-groupe utilisé:
| Taux d’infection ► ▼ Taille du Mini-Groupe |
0.5% | 1% | 2% | 3% | 5% | 8% | 10% | 20% | 50% |
| 2 | 0.51 | 0.51 | 0.53 | 0.54 | 0.57 | 0.62 | 0.64 | 0.78 | 1.12 |
| 4 | 0.26 | 0.28 | 0.31 | 0.34 | 0.39 | 0.48 | 0.53 | 0.77 | 1.30 |
| 8 | 0.15 | 0.17 | 0.21 | 0.25 | 0.33 | 0.45 | 0.52 | 0.82 | 1.41 |
| 16 | 0.09 | 0.12 | 0.18 | 0.23 | 0.33 | 0.46 | 0.54 | 0.87 | 1.47 |
| 32 | 0.07 | 0.10 | 0.17 | 0.23 | 0.34 | 0.48 | 0.57 | 0.90 | 1.51 |
4. Questions ouvertes
Il reste des questions ouvertes intéressantes à explorer. En particulier, si les tests ne sont pas 100% précis, quel est le meilleur moyen de réduire les erreurs en utilisants plusieurs tests croisés ? Comment généraliser ces formules à des mini-groupes qui ne sont pas des puissances de 2 ? Je laisse ces questions aux lecteurs intéressés, et je reviendrai peut être dessus dans un futur billet de blog 😉
Courage et prudence à tous !