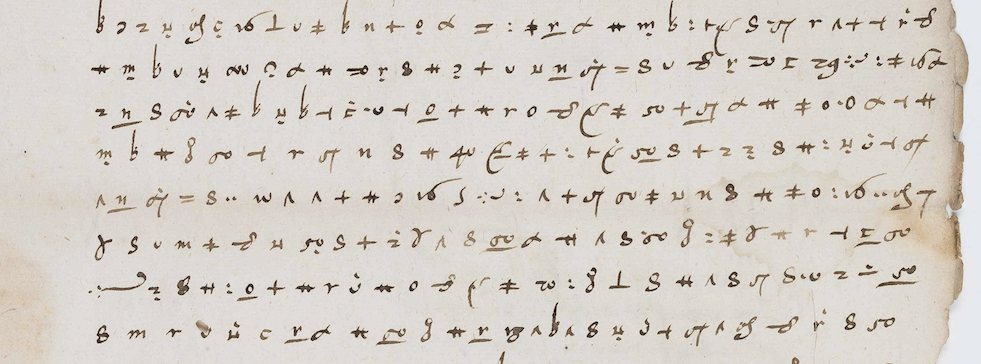
Back In Time

BACK IN TIME est une action exploratoire soutenue et financée par Inria.

Soyez prêts à découvrir des complots inattendus et à déterrer des secrets vieux comme le monde ! BACK IN TIME est la mise en relation des expertises de chercheurs de trois domaines – intelligence artificielle, cryptographie et histoire – afin de décrypter des documents historiques chiffrés, parfois restés endormis depuis plusieurs siècles. Le nombre de pages et la variété des symboles et des règles étant importants, nous souhaitons mettre au point un premier logiciel pour l’aide voire l'automatisation des déchiffrements de l'histoire antique, médiévale et moderne.

Ce projet a débuté en 2024. Il est mené en collaboration avec l'équipe Almanach, une équipe Inria à Paris, ainsi qu'avec une chercheuse en histoire Camille Desenclos.
Pour plus d'information, vous pouvez lire l'article de présentation ici.