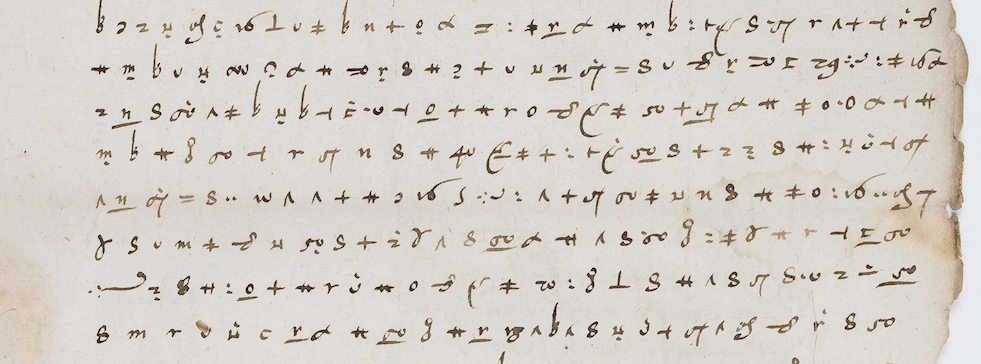
Back In Time

Back In Time is an exploratory project supported and funded by Inria.

Get ready to uncover unexpected plots and unearth secrets as old as time! Back In Time brings together the expertise of researchers in three fields - artificial intelligence, cryptography and history - to decipher encrypted historical documents, some of which have lain dormant for several centuries. Given the sheer number of pages and the variety of symbols and rules involved, our aim is to develop the first software programme to assist or even automate the decoding of ancient, medieval and modern history.

This project began in 2024. It is being carried out in collaboration with the Almanach team, an Inria team in Paris, and a history researcher, Camille Desenclos.