Subsections
Optimization features
This section describes the features that allow MSVMpack to make use of the full resources of the computer in terms of CPU and memory. The basic idea is to reduce the computational burden of kernel function evaluations by acting at three different levels:
- multiple kernel function values are computed in parallel,
- computed kernel values are cached in memory (as much as possible),
- kernel functions are optimized (vectorized) for faster evaluations.
Putting these three features together results in a training algorithm which is less limited by the latency of kernel function evaluations. In practice, each training step (except the first one) starts with kernel values that either have been already computed in parallel during the previous step or are stored in cache memory. Thus, the limiting factor becomes the time of the computations required by the optimization step. The most intensive task in this step is the update of the gradient vector, which is also parallelized in MSVMpack.
Note that the behavior described above can only be observed when using a computer with enough memory or CPUs (cores). However, the implemented scheme allows MSVMpack to compensate a lack of memory by using more CPUs or to remain efficient with few CPUs by using extra memory.
Parallel implementation
MSVMpack offers a parallel implementation of the training algorithms of the four M-SVMs (WW, CS, LLW, M-SVM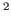 ). This parallelization takes place at the level of a single computer to make use of multiple CPUs (or cores) and is not designed for cluster computing across multiple computers.
). This parallelization takes place at the level of a single computer to make use of multiple CPUs (or cores) and is not designed for cluster computing across multiple computers.
The main parameter of this implementation is the number of working threads. For best performance, this number should correspond to the number of available CPUs (or cores). By default, trainmsvm and predmsvm will automatically detect the number of CPUs at run time, but a particular number N can be enforced with the -t option, e.g., as in
trainmsvm myTrainingData myMSVM.model -t N
This can be useful on architectures that include hyperthreading, for which the system typically assumes a number of CPUs that is twice the number of physical CPUs (or cores).
The implementation follows a simple design with a rather coarse granularity, in which kernel computations are parallelized. These computations are the most intensive ones compared to training steps and model updates. In addition, they only depend on the training data, which is constant throughout training. It is thus possible to compute multiple kernel function values at the same time or while a model update is performed. In summary, the program creates a number of working threads which implement the following scheme (in which the steps running in parallel are shown in italic).
- Select a random chunk of data.
- Compute the kernel submatrix corresponding to this data chunk.
- Wait for the M-SVM model to become available (in case another thread is currently updating the model).
- Take a training step and update the model.
- Release the model (to unblock waiting threads).
- Loop from step 1 until training is stopped.
Note that, for the CS model type, the data chunk selection is not random and actually makes use of the model (see section 4.2). In this case, it cannot be easily parallelized and the scheme above is modified to select the working set for the next training step between steps 4 and 5, while step 6 loops only from step 2.
Assuming a number of threads equal to the number of CPUs, a thread can be blocked waiting in step 5 for at most
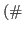 CPUs
CPUs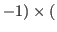 time required by a training step
time required by a training step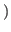 . In most cases, this quantity is rather small compared to the time required to compute the kernel submatrix. This results in a high working/idle time ratio. However, a small additional delay can be observed when MSVM_eval() is called (every 1000 iterations) to evaluate the criterion (1). This is particularly true for the M-SVM
. In most cases, this quantity is rather small compared to the time required to compute the kernel submatrix. This results in a high working/idle time ratio. However, a small additional delay can be observed when MSVM_eval() is called (every 1000 iterations) to evaluate the criterion (1). This is particularly true for the M-SVM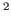 , for which the computation of the upper bound on the optimum is more involved due to the form of the primal objective function.
, for which the computation of the upper bound on the optimum is more involved due to the form of the primal objective function.
The next most intensive computation is the update of the gradient vector after each training step. This computation is parallelized by splitting the gradient vector in several parts, each one of which is updated in a separate thread. For best efficiency, MSVMpack maintains the number of working threads equal to the number of CPUs. At the beginning of training, all working threads apply the procedure above to compute kernel function values in parallel and a single thread (the one that is currently in step 4) is used to compute the gradient updates3. As training goes, kernel values are cached (see section 4.3 below) and the work load of kernel computations decreases. Former working threads are thus stopped and more threads are used to update the gradient4. If the kernel matrix fits in memory, then all CPU resources are eventually assigned to these gradient updates.
The classification function MSVM_classify_set() (used by predmsvm) is also parallelized to increase the speed of predictions on large test sets. The approach is rather straightforward: the test set is cut into subsets of size SET_SIZE (constant defined in libevalMSVM.h) and the model output is computed on each subset in a separate thread.
The K-fold cross validation procedure (called with -cv K) requires training of K models and can also be parallelized with two possible scenarios. In case the number of CPUs is larger than the number of models to be trained, each one of the K models is trained in parallel with
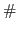 CPUs
CPUs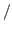 K working threads applying the scheme above to compute the kernel function values and gradient updates. Otherwise, the first
K working threads applying the scheme above to compute the kernel function values and gradient updates. Otherwise, the first
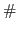 CPUs models are trained in parallel with a single working thread and the next one starts training as soon as the first one is done, and so on.
When all models are trained, the K test subsets are classified sequentially, but nonetheless efficiently thanks to the parallelization of the classification function MSVM_classify_set() described above.
CPUs models are trained in parallel with a single working thread and the next one starts training as soon as the first one is done, and so on.
When all models are trained, the K test subsets are classified sequentially, but nonetheless efficiently thanks to the parallelization of the classification function MSVM_classify_set() described above.
We used POSIX threads (Pthreads) to implement parallelism on shared memory multiprocessor architectures. POSIX threads constitute the IEEE/The Open Group standard for thread implementation available across many platforms. However, this choice leads to the need for a specific port of the software for Windows platforms. Windows users can read about the Pthreads-win32 project at http://sourceware.org/pthreads-win32/ for a possible alternative solution (not tested).
Working set selection
Most implementations of SVM learning algorithms include a dedicated working set selection procedure that determines the subset of variables that will be optimized in the next training step. Such procedures are of particular importance in order to reduce the numbers of iterations and of kernel evaluations required by the algorithm. In addition, these methods typically lead to convergence without having to optimize over all variables (not even for one training step). In such cases, only a small subset of the kernel matrix need to be computed, thus limiting the amount of memory required for kernel cache (see section 4.3).
MSVMpack includes the working set selection strategy proposed in [2] in order to choose the chunk of data considered in the next optimization step. This strategy is based on the Karush-Kuhn-Tucker (KKT) conditions of optimality applied to the dual problem. The data points with maximal violation of the KKT conditions are selected. This violation can be measured for each data point
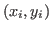 by5
by5
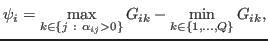 |
(2) |
where 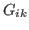 is the gradient with respect to
is the gradient with respect to
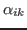 of the dual objective function being minimized.
of the dual objective function being minimized.
In practice, the conditions
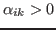 involved in the computation of the maximum in
involved in the computation of the maximum in 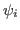 has to be tested up to a given precision with a threshold. However, note that, contrary to other implementations that typically use
has to be tested up to a given precision with a threshold. However, note that, contrary to other implementations that typically use
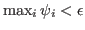 as a stopping criterion, MSVMpack stops the algorithm on the basis of the ratio (1) and uses
as a stopping criterion, MSVMpack stops the algorithm on the basis of the ratio (1) and uses 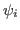 only for working set selection. Thus, the value chosen for the threshold does not influence the quality of the solution obtained at the end of training (but can however influence the speed of convergence to that solution).
only for working set selection. Thus, the value chosen for the threshold does not influence the quality of the solution obtained at the end of training (but can however influence the speed of convergence to that solution).
Unfortunately, there is no simple measure of the violation of the KKT conditions for the other M-SVM models. Thus, for these models, MSVMpack uses a random selection procedure for the next data points to consider in the chunk.
Note that the implementation of Weston and Watkins model as proposed in [6] for the BSVM software does include a working set selection strategy. However, this strategy relies on a modification of the optimization problem in which the term
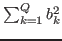 is also minimized. MSVMpack solves the original form of the problem as proposed in [11] and thus cannot use a similar strategy.
is also minimized. MSVMpack solves the original form of the problem as proposed in [11] and thus cannot use a similar strategy.
Kernel cache
MSVMpack can use extra memory to cache the kernel matrix (or a subset of it). Note that, in comparison with other SVM implementations, working set selection in MSVMpack is based on a random selection of a data chunk (except for the CS type, see section 4.2) and no shrinking is performed (see for instance [1] for a definition of shrinking and more information on other implementations). As a result, the software may store the entire kernel matrix if it fits in memory, so that large cache memory sizes will help to deal with large data sets (other implementations with proper working set selection and/or shrinking typically require much fewer kernel evaluations and cache memory).
By default, training algorithms use the entire physical memory minus 1 GByte for kernel caching, but this can be changed from the command line with the -x option. For instance:
trainmsvm myDataFile -x 4096
will set the maximal amount of kernel cache memory to 4 GBytes.
The kernel cache maintains a list of the kernel matrix rows that are already cached. When a worker thread needs a particular row, the following three cases can occur.
- The row is already cached and available: the worker thread gets a pointer to this row in cache memory.
- The row is not available in cache: the worker thread computes the row in cache memory and then uses a pointer to this row.
- The row is not available in cache but another thread is currently computing it: the worker thread waits for the computation of the row to terminate and then gets a pointer to this row in cache memory.
If the cache memory size is not sufficient to store the entire kernel matrix, rows are dropped from the cache when new ones need to be computed and stored.
In the parallelized cross validation procedure described in Sect. 4.1, many kernel computations can be saved as the K models are trained in parallel from overlapping subsets of the data set. More precisely, MSVMpack implements the following scheme.
A master kernel cache stores complete rows of the global kernel matrix computed from the entire data set.
For each one of the K models, a local kernel cache stores rows of a kernel submatrix computed with respect the corresponding training subset.
When a working thread requests a row that is not currently in the local kernel cache, the request is forwarded to the master cache which returns the complete row with respect to the entire data set. Then, the elements of this row are mapped to a row of the local cache. This mapping discards the columns corresponding to test data for the model and takes care of the data permutation used to generate the training subsets at the beginning of the cross validation.
In this scheme, every kernel computation performed by a working thread to train a particular model benefits to other models as well. In the case where the entire kernel matrix fits in memory, all values are computed only once to train K models.
Data format-specific and vectorized kernel functions
In many cases, data sets processed by machine learning algorithms contain real numbers with no more than 7 significant digits (which is often the default when writing real numbers to a text file) or even integer values. On the other hand, the typical machine learning software loads and processes these values as double precision floating-point data, which is a waste of both memory and computing time.
MSVMpack can handle data in different formats and use a different kernel function for each format. This may be used for instance to increase the speed of kernel computations on single precision floats or integers. Note that, in a kernel computation
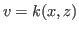 , only the format of
, only the format of 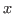 and
and 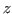 changes and the resulting value
changes and the resulting value 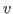 is always in double precision floating-point format. All other computations in the training algorithms also remain double-precision.
is always in double precision floating-point format. All other computations in the training algorithms also remain double-precision.
Table 3:
Data format options for trainmsvm.
| Option flag |
Data format |
|---|
| none (default) |
double precision floating-point (64-bit) |
| -f |
single precision floating-point (32-bit) |
| -I |
32-bit integer |
| -i |
16-bit short integer |
| -B |
byte (8-bit unsigned integer) |
| -b |
bit (all non-zero values are considered as 1) |
The data format can be chosen from the command line by using the appropriate option according to Table 3. E.g., for single precision floating-point data format:
trainmsvm mySinglePrecisionData -m WW -k 2 -f
In this example, the data are loaded in memory as single-precision floats and the kernel function (the Gaussian RBF in this example) may be computed faster (see below).
Proper data alignment in memory allows MSVMpack to use vectorized implementations of kernel functions when compiled on SSE4.2, SSE4.1, SSE3 or SSE2 capable processors. These implementations make use of the SIMD (Single Instruction Multiple Data) instruction sets available on such processors to process multiple components of large data vectors simultaneously. Note that this is mostly effective for small data formats such as single-precision floats or short integers.
lauer
2014-07-03
![]() ). This parallelization takes place at the level of a single computer to make use of multiple CPUs (or cores) and is not designed for cluster computing across multiple computers.
). This parallelization takes place at the level of a single computer to make use of multiple CPUs (or cores) and is not designed for cluster computing across multiple computers.
![]() CPUs
CPUs![]() time required by a training step
time required by a training step![]() . In most cases, this quantity is rather small compared to the time required to compute the kernel submatrix. This results in a high working/idle time ratio. However, a small additional delay can be observed when MSVM_eval() is called (every 1000 iterations) to evaluate the criterion (1). This is particularly true for the M-SVM
. In most cases, this quantity is rather small compared to the time required to compute the kernel submatrix. This results in a high working/idle time ratio. However, a small additional delay can be observed when MSVM_eval() is called (every 1000 iterations) to evaluate the criterion (1). This is particularly true for the M-SVM![]() , for which the computation of the upper bound on the optimum is more involved due to the form of the primal objective function.
, for which the computation of the upper bound on the optimum is more involved due to the form of the primal objective function.
![]() CPUs
CPUs![]() K working threads applying the scheme above to compute the kernel function values and gradient updates. Otherwise, the first
K working threads applying the scheme above to compute the kernel function values and gradient updates. Otherwise, the first
![]() CPUs models are trained in parallel with a single working thread and the next one starts training as soon as the first one is done, and so on.
When all models are trained, the K test subsets are classified sequentially, but nonetheless efficiently thanks to the parallelization of the classification function MSVM_classify_set() described above.
CPUs models are trained in parallel with a single working thread and the next one starts training as soon as the first one is done, and so on.
When all models are trained, the K test subsets are classified sequentially, but nonetheless efficiently thanks to the parallelization of the classification function MSVM_classify_set() described above.
![]() by5
by5
![]() involved in the computation of the maximum in
involved in the computation of the maximum in ![]() has to be tested up to a given precision with a threshold. However, note that, contrary to other implementations that typically use
has to be tested up to a given precision with a threshold. However, note that, contrary to other implementations that typically use
![]() as a stopping criterion, MSVMpack stops the algorithm on the basis of the ratio (1) and uses
as a stopping criterion, MSVMpack stops the algorithm on the basis of the ratio (1) and uses ![]() only for working set selection. Thus, the value chosen for the threshold does not influence the quality of the solution obtained at the end of training (but can however influence the speed of convergence to that solution).
only for working set selection. Thus, the value chosen for the threshold does not influence the quality of the solution obtained at the end of training (but can however influence the speed of convergence to that solution).
![]() is also minimized. MSVMpack solves the original form of the problem as proposed in [11] and thus cannot use a similar strategy.
is also minimized. MSVMpack solves the original form of the problem as proposed in [11] and thus cannot use a similar strategy.
![]() , only the format of
, only the format of ![]() and
and ![]() changes and the resulting value
changes and the resulting value ![]() is always in double precision floating-point format. All other computations in the training algorithms also remain double-precision.
is always in double precision floating-point format. All other computations in the training algorithms also remain double-precision.