Qu'y a-t-il dans ce donjon ?
Les
documents disponibles sur cette page ainsi que le contenu de la page
sont mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International 
Cette activité a été créée par Mathieu Tabary lors de son stage de L3. Vous pouvez trouver la version originale sur son Github
Notions abordées :
Cette activité a pour but de faire découvrir les algorithmes de parcours de graphes en largeur et en profondeur. Elle peut être utilisée comme première approche pour les graphes et permettre de travailler la formulation d'algorithmes.
Public :
Cette activité a été conçue pour des lycéens découvrant les graphes ainsi que les algorithmes les concernant. Si on se limite à la découverte des parcours sans formalisation, on peut aborder l'activité plus tôt. Cela a été fait avec une élève de primaire (CM2), de deux collégiennes (5ème). Un test par visioconférence a également été fait auprès du public cible : des lycéens n'ayant pas encore étudié les graphes et les algorithmes de parcours.
Matériel :
 Le matériel nécesssaire est assez limité :
Le matériel nécesssaire est assez limité :
- feuilles + stylo
- un jeton pour marquer où est le personnage dans le donjon
- des graphes représentant le plan d'un donjon. Un certain nombre d'exemples imprimables est disponible dans la section Liens
Principe :
Cette activité s'inspire de jeux de rôle du
genre Dungeon
Crawler, où le joueur doit explorer et cartographier son
environnement.
Elle va se faire par groupes de deux ou trois
personnes, l'une incarnant le maître du jeu, qui connaît le plan
du donjon, et le ou les autres jouant les aventuriers, dont le
but est de visiter tout le donjon et d'y trouver les trésors. Les participants changeront de rôle au cours de l'activité.
Voici une proposition de déroulé pour l'activité :
- Le maître du jeu reçoit la carte d'un donjon que lui seul à le droit de voir. Les aventuriers commencent dans la salle d'entrée, et le maître du jeu leur indique juste les portes qui en sortent et leur orientation. Les aventuriers choisissent quelle porte emprunter et le maître du jeu leur indique dans quelle salle mène ce couloir ainsi que les portes qui en sortent. L'objectif des aventuriers est de découvrir tout le donjon.
- Une fois les règles intéfgrées, on change les rôles et sur un nouveau donjon on ajoute le jeton. Au fur et à mesure de l'exploration, les aventuriers déplacent un jeton de salle en salle, et comptent le nombre de couloirs empruntés. Le but est toujours de découvrir tout le donjon, mais en essayant de ne pas parcourir inutilement des couloirs en tout sens.
- On passe ensuite à la formalisation : chaque groupe doit proposer une méthode (donc un algorithme) qui leur permettrait d'expliquer à l'un de leur camarades comment explorer tout le donjon. Ils passent ensuite leur algorithme à un autre groupe done l'objectif est de le tester et dire s'il fonctionne ou pas. L'utilisation du jeton et l'objectif de limiter le nombre de déplacements risque d'amener à un parcours du type "en profondeur".
Extensions :
Il est possible de décliner cette activité afin de faire découvrir d'autres algorithmes et théories sur les graphes. Par exemple :
- pour faire découvrir le parcours en largeur, on peut retirer la contrainte sur le nombre de déplacement (en imaginant que les aventuriers peuvent se téléporter dans toute salle déjà visitée), et demander aux élèves de trouver la plus courte distance (en termes de nombre de couloirs) depuis l'entrée vers n'importe quelle salle,
- on peut pour compliquer un peu les choses utiliser des graphes non planaires, par exemple pour représenter un donjon à plusieur étages,
- on peut également parler de graphes pondérés en ne considérant plus un coût de 1 pour chaque couloir emprunté mais en donnant une valeur à chaque couloir (le temps que cela prend de le traverser). Sur un tel graphe on cherche un chemin à coût minimum depuis l'entrée vers chaque salle.
Liens :
La plupart des liens mentionnés ci-dessous est accessible sur le Github de Mathieu, l'auteur de cette activité. Je les ai hébergés sur ma page pour éviter les problèmes de liens non à jour.- Vous trouverez le document de Mathieu décrivant l'activité en détails ici avec un exemple d'exploration d'un donjon assez petit, une explication sur les distances à exprimer pour les couloirs fourbes (=avec des virages), ainsi qu'un algorithme de parcours en profondeur et un agorithme de parcours en largeur, tout deux utilisés pour faire les "corrections" des parcours des donjons,
- vous pouvez imprimer une liste de donjons faciles,
- il y a également une liste de donjons moyens,
- et enfin un donjon plus difficile.
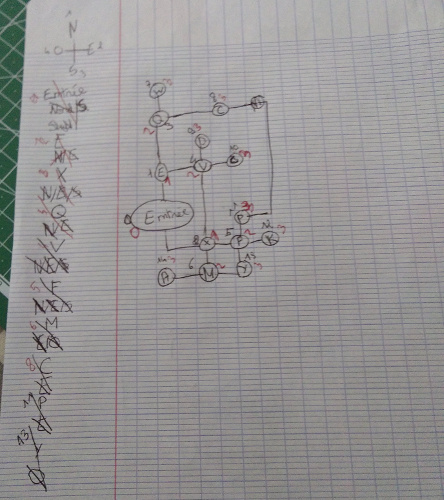
Photos :
De gauche à droite : deux collégiennes testant l'activité à distance grâce à une caméra directionnelle, un deuxième test en visio, et le résultat de l'application du parcours en largeur par une élève de CM2.