21 Réseaux de neurones

Un réseau de neurones est un modèle de prédiction adapté à la classification ou la régression.

Son architecture est définie par un graphe orienté dans lequel les connexions entre les nœuds sont pondérées. Chaque nœud est un neurone artificiel qui implémente un calcul simple pour produire une sortie à partir de ses entrées.

Les neurones sont typiquement organisés en couches qui peuvent être de différents types.

21.1 Unité de calcul de base : le neurone (artificiel)

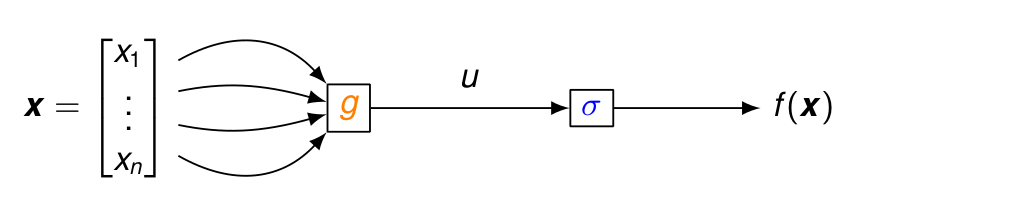
Un neurone artificiel implémente la fonction f(\boldsymbol{z}) = \sigma\left(\sum_{k=1}^n w_k z_k + b\right) = \sigma(\boldsymbol{w}^T \boldsymbol{z} + b) = \sigma(u) où

\boldsymbol{z}\in\mathbb{R}^n est le vecteur des entrées
\boldsymbol{w}\in\mathbb{R}^n est le vecteur des poids (paramètre à apprendre)
b est le terme de biais (paramètre à apprendre)
\sigma est la fonction d’activation
u est le niveau d’activation (somme pondérée des entrées)

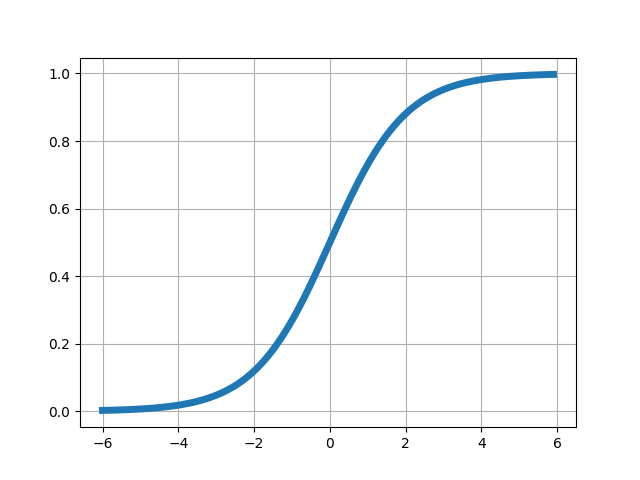
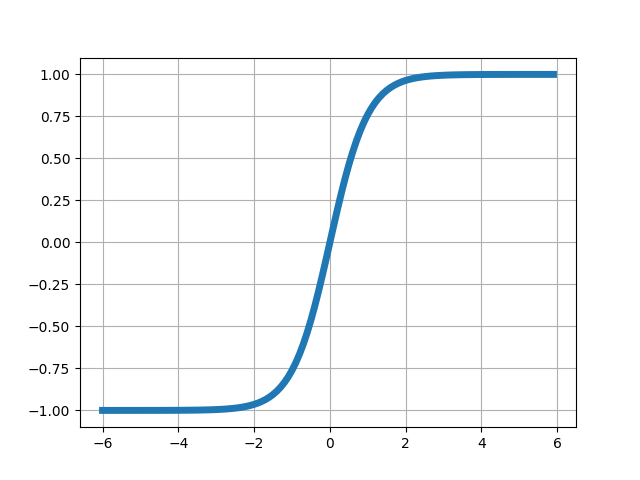
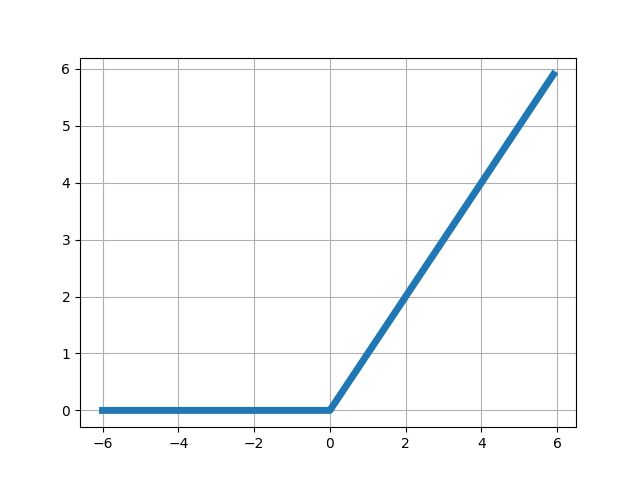
Il existe beaucoup de fonctions d’activation différentes, dont certaines peuvent originellement être vues comme des approximations lisses et dérivables de la fonction seuil utilisée par le perceptron. Voici les plus courantes :

sigmoïde : \sigma(u) = \frac{1}{1+e^{-u}}

21.2 Perceptron multicouches (MLP)

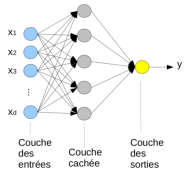
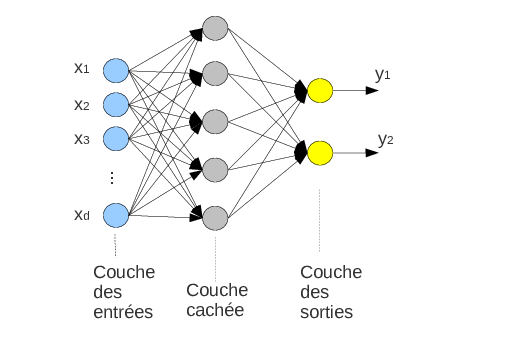
Le perceptron multicouches (multilayer perceptron, MLP) est le réseau de neurones le plus simple, composé de couches denses, c’est-à-dire des couches de neurones dans lesquelles chaque neurone est connecté à tous les neurones de la couche précédente par ses entrées et tous ceux de la couche suivante par sa sortie.

Un réseau de neurones peut aisément prédire plusieurs étiquettes simultanément en ajoutant des neurones sur sa dernière couche, appelée couche de sortie. Les couches intermédiaires entre les entrées et les sorties sont appelées couches cachées, car le réseau de neuronne peut être vu comme un modèle « boîte noire » dont le comportement interne n’est pas nécessairement représentatif du processus modélisé.

En général, tous les neurones d’une couche sont du même type (avec la même fonction d’activation), mais ils peuvent être différents d’une couche à l’autre.

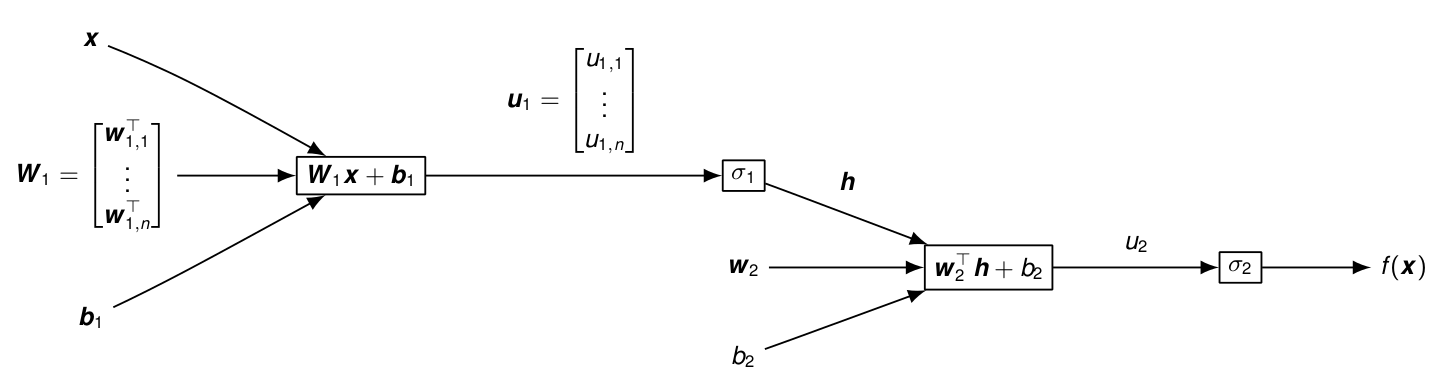
La fonction calculée par le réseau se définit alors de manière récursive par composition, par exemple : f(\boldsymbol{x}) = \sigma_2\left( \boldsymbol{w}_2^T \sigma_1(\boldsymbol{W}_1 \boldsymbol{x} + b_1) + b_2\right) où \sigma_1, \boldsymbol{W}_1, \boldsymbol{b}_1 sont la fonction d’activation et les paramètres de l’unique couche cachée et \sigma_2, \boldsymbol{w}_2, b_2 ceux utilisés par la couche de sortie. Ici, \boldsymbol{u}_1 = \boldsymbol{W}_1 \boldsymbol{x} + b_1 représente le niveau d’activation de l’ensemble des n neurones de la couche cachée de paramètres \boldsymbol{W}_1 = \begin{bmatrix}\boldsymbol{w}_{1,1}^T\\\vdots\\\boldsymbol{w}_{1,n}^T\end{bmatrix},\ \boldsymbol{b}_1=\begin{bmatrix}b_{1,1}\\\vdots\\b_{1,n}\end{bmatrix} où \boldsymbol{w}_{1,j}, b_{1,j} sont les paramètres du jème neurone de cette couche.

De manière résumée, l’apprentissage d’un réseau de neurones revient à déterminer la structure du réseau et les valeurs des poids (et biais) affectés aux connexions. En général, cela se fait en deux temps :

fixer la structure du réseau et choisir les fonctions d’activations ;
calculer les poids de manière à minimiser les erreurs de prédiction sur la base d’apprentissage.

21.2.1 Apprentissage des poids : minimisation de l’erreur sur les données

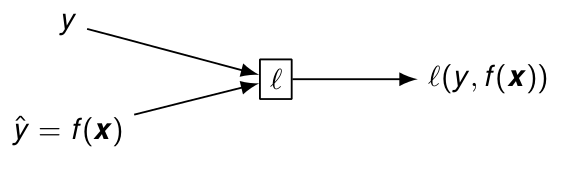
L’apprentissage des poids d’un réseau de neurones vise à sélectionner les paramètres qui conduisent à la meilleure prédiction possible sur la base d’aprentissage. Pour une fonction de perte \ell, par exemple \ell(y_i, f(\boldsymbol{x}_i)) = (y_i - f(\boldsymbol{x}_i))^2 pour la régression, l’apprentissage revient à résoudre le problème d’optimisation \min_{\boldsymbol{w}} J(\boldsymbol{w}) = \sum_{i=1}^m \ell(y_i, f(\boldsymbol{x}_i)) où f représente la fonction calculée par le réseau de neurones et \boldsymbol{w} concatène tous ses paramètres (y compris les biais).

La méthode de base utilisée pour minimiser l’erreur est la descente de grandient, car c’est une des méthodes les plus simples pour minimiser une fonction sans contraintes. Par ailleurs, la taille des réseaux de neurones (et la dimension du problème d’optimisation) empêche bien souvent d’utiliser des méthodes plus avancées basées sur les dérivées du second ordre par exemple.

À l’inverse, la descente de gradient ne nécessite que le calcul des dérivées premières et consiste à appliquer les itérations \boldsymbol{w} \leftarrow \boldsymbol{w} - \mu \frac{\text{d} J(\boldsymbol{w})}{\text{d} \boldsymbol{w}}= \boldsymbol{w} - \sum_{i=1}^m \mu \frac{\text{d} \ell(y_i, f(\boldsymbol{x}_i))}{\text{d} \boldsymbol{w}} où \mu\in(0,1) est un hyperparamètre appelé taux d’apprentissage.

Cependant, ces itérations requièrent le calcul de m dérivées à chaque itération, ce qui peut se révéler trop fastidieux sur les jeux de données avec un grande nombre m d’exemples.

21.2.2 Descente de gradient stochastique

La descente de gradient stochastique offre une approximation de la descente de gradient permettant d’accélérer les itérations. L’idée est simple : au lieu de calculer le gradient de l’erreur totale, chaque itération ne s’intéresse qu’à l’erreur sur un seul exemple : pour i tiré aléatoirement dans \{1,\dots,m\}, \boldsymbol{w} \leftarrow \boldsymbol{w} - \mu \frac{\text{d} \ell(y_i, f(\boldsymbol{x}_i))}{\text{d} \boldsymbol{w}}

Les calculs sont ici beaucoup plus légers à chaque itération, mais la convergence peut nécessiter en contrepartie beaucoup plus d’itérations.

21.2.3 Calcul des dérivées et rétropropagation du gradient

Dans un réseau de neurones, les calculs de dérivées peuvent être largement optimisés dans le cadre de la rétropropagation du gradient.

21.2.3.1 Dérivées en chaîne (avec une seule variable)

Composition de deux fonctions d’une variable

Pour f(x) = \sigma(u) = \textcolor{blue}{\sigma(}\ \textcolor{orange}{g(}x\textcolor{orange}{)} \ \textcolor{blue}{)},\quad avec\ u=g(x) la règle de dérivation en chaîne donne \frac{\text{d} f(x)}{\text{d} x} =\textcolor{blue}{\frac{\text{d} f(x)}{\text{d} u}}\textcolor{orange}{\frac{\text{d} u}{\text{d} x}} = \textcolor{blue}{\sigma'(u)}\textcolor{orange}{g'(x)}

Exemple : calculer \frac{\text{d} f(x)}{\text{d} x} pour f(x) = \textcolor{blue}{(}\textcolor{orange}{5-3x}\textcolor{blue}{)^2} = u^2,\quad u=g(x)=5-3x

Solution

\textcolor{blue}{\sigma'(u) = 2u},\quad \textcolor{orange}{g'(x)=-3} \Rightarrow\quad \frac{\text{d} f(x)}{\text{d} x} = -6(5-3x)

Avec plusieurs compositions : Composition de trois fonctions d’une variable

f(x) = \textcolor{blue}{\sigma(}\ \textcolor{orange}{g(}\ \textcolor{green}{h(}x\textcolor{green}{)}\ \textcolor{orange}{)}\ \textcolor{blue}{)} = \sigma(u), \quad u=g(v),\quad v=h(x) \Rightarrow \frac{\text{d} f(x)}{\text{d} x} =\textcolor{blue}{\frac{\text{d} f(x)}{\text{d} u}}\textcolor{brown}{\frac{\text{d} u}{\text{d} x}} = \textcolor{blue}{\frac{\text{d} f(x)}{\text{d} u}}\textcolor{orange}{\frac{\text{d} u}{\text{d} v}}\textcolor{green}{ \frac{\text{d} v}{\text{d} x}} = \textcolor{blue}{\sigma'(u)}\textcolor{orange}{ g'(v)}\textcolor{green}{ h'(x)} Si la dérivée de f par rapport à u ou à v a déjà été calculée, on peut donc économiser des calculs.

Exemple : calculer \frac{\text{d} f(x)}{\text{d} x} pour f(x) = \textcolor{blue}{(}\textcolor{orange}{5-3}\textcolor{green}{e^{-4x}} \textcolor{blue}{)^2} = u^2,\quad u= 5-3 v,\quad v=h(x)=e^{-4x}

Solution

\textcolor{blue}{\sigma'(u) = 2u},\quad \textcolor{orange}{g'(v) = -3},\quad \textcolor{green}{h'(x) =-4e^{-4x}} \Rightarrow \quad \frac{\text{d} f(x)}{\text{d} x} = 24e^{-4x}(5-3e^{-4x})

Avec plusieurs chemins :

Composition avec plusieurs chemins 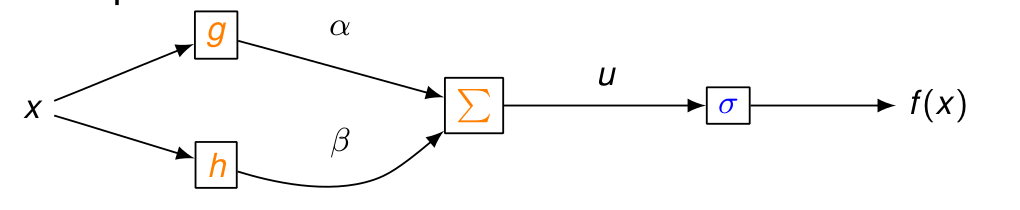f(x) = \sigma(u) ,\quad u = \alpha g(x) + \beta h(x) \Rightarrow \frac{\text{d} f(x)}{\text{d} x} =\textcolor{blue}{\frac{\text{d} f(x)}{\text{d} u}}\textcolor{orange}{ \frac{\text{d} u}{\text{d} x}} = \textcolor{blue}{\sigma'(u)} \textcolor{orange}{ \left( \alpha g'(x) + \beta h'(x) \right)} Exemple : calculer \frac{\text{d} f(x)}{\text{d} x} pour f(x) = \textcolor{blue}{\exp\left(\textcolor{orange}{ 2(5-3x)^2 + 0.5 (2+3x)^3} \right)} = \exp(u) = \sigma(u), \quad g(x) = (5-3x)^2,\quad h(x) = (2+3x)^3, \quad \alpha = 2, \ \beta = 0.5

Solution

\textcolor{blue}{\sigma'(u) = \exp(u)}, \quad g'(x) = -6(5-3x) ,\quad h'(x) = 9(2+3x)^2 \frac{\text{d} f(x)}{\text{d} x} = \exp\left( 2(5-3x)^2 + 0.5 (2+3x)^3 \right) \left(-12(5-3x) + 4.5(2+3x)^2 \right)

21.2.3.2 Calcul de gradients en chaîne

Composition de fonctions de plusieurs variables

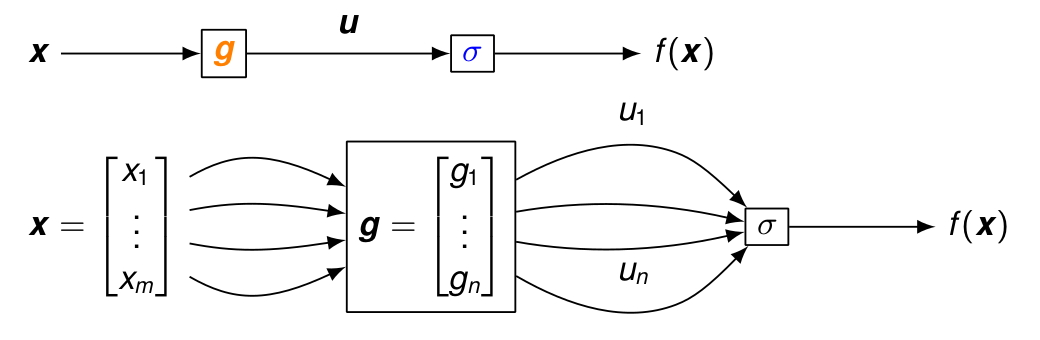
Pour f(\boldsymbol{x}) = \textcolor{blue}{\sigma(}\ \textcolor{orange}{g(}\boldsymbol{x}\textcolor{orange}{)}\ \textcolor{blue}{)} = \sigma(u),\quad avec\ u=g(\boldsymbol{x})=g(x_1,\dots,x_n) avec plusieurs variables, la dérivée devient un gradient, mais les règles de composition restent identiques car elles s’appliquent aux dérivées partielles : \frac{\partial f(\boldsymbol{x})}{\partial x_k} =\textcolor{blue}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} u}}\textcolor{orange}{\frac{\partial u}{\partial x_k}} \quad \Rightarrow \frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{x}} =\textcolor{blue}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} u}}\textcolor{orange}{\frac{\text{d} u}{\text{d} \boldsymbol{x}}} = \textcolor{blue}{\sigma'(u)} \textcolor{orange}{\frac{\text{d} g(\boldsymbol{x})}{\text{d} \boldsymbol{x}}}

Exemple : calculer le gradient de f pour f(\boldsymbol{x}) = \textcolor{blue}{(}\textcolor{orange}{5x_1-3x_1 x_2}\textcolor{blue}{)^2} = u^2,\quad u=g(\boldsymbol{x})=5x_1-3x_1x_2

Solution

\textcolor{blue}{\sigma'(u) = 2u},\quad \textcolor{orange}{\frac{\text{d} g(\boldsymbol{x})}{\text{d} \boldsymbol{x}} =\begin{bmatrix}5 - 3 x_2\\-3 x_1\end{bmatrix}} \Rightarrow\quad \frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{x}} = 2 (5x_1-3x_1 x_2) \begin{bmatrix}5 - 3 x_2\\-3 x_1\end{bmatrix}

Pour la composition avec une fonction à valeur vectorielle :

Composition avec une fonction vectorielle

f(\boldsymbol{x}) = \textcolor{blue}{\sigma(}\ \textcolor{orange}{\boldsymbol{g}(}\ \boldsymbol{x}\ \textcolor{orange}{)}\ \textcolor{blue}{)} = \sigma(\boldsymbol{u}) = \sigma(u_1,\dots, u_n), \quad \boldsymbol{u}=\boldsymbol{g}(\boldsymbol{x}) = \begin{bmatrix}g_1(x_1,\dots,x_m)\\\vdots\\g_n(x_1,\dots,x_m)\end{bmatrix} La dérivée partielle de f(\boldsymbol{x}) par rapport à x_k est donnée par la somme sur tous les chemins de x_k à f(\boldsymbol{x}) : \frac{\partial f(\boldsymbol{x})}{\partial x_k} = \sum_{j=1}^n \frac{\partial f(\boldsymbol{x})}{\partial u_j} \frac{\partial u_j}{\partial x_k} = \begin{bmatrix}\frac{\partial u_1}{\partial x_k} & \dots & \frac{\partial u_n}{\partial x_k} \end{bmatrix} \begin{bmatrix}\frac{\partial f(\boldsymbol{x})}{\partial u_1} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial u_n} \end{bmatrix} \Rightarrow \frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{x}}= \begin{bmatrix}\frac{\partial f(\boldsymbol{x})}{\partial x_1} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial x_m} \end{bmatrix}= \begin{bmatrix}\frac{\partial u_1}{\partial x_1} & \dots & \frac{\partial u_n}{\partial x_1} \\\vdots & & \vdots \\\frac{\partial u_1}{\partial x_m} & \dots & \frac{\partial u_n}{\partial x_m} \end{bmatrix} \begin{bmatrix}\frac{\partial f(\boldsymbol{x})}{\partial u_1} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial u_n} \end{bmatrix} En introduisant la matrice jacobienne, \frac{\text{d} \boldsymbol{u}}{\text{d} \boldsymbol{x}} = \begin{bmatrix}\left(\frac{\text{d} u_1}{\text{d} \boldsymbol{x}}\right)^\top \\\vdots\\\left(\frac{\text{d} u_n}{\text{d} \boldsymbol{x}}\right)^\top \end{bmatrix} = \begin{bmatrix}\frac{\partial u_1}{\partial x_1} & \dots & \frac{\partial u_1}{\partial x_m}\\\vdots & & \vdots\\\frac{\partial u_n}{\partial x_1} & \dots & \frac{\partial u_n}{\partial x_m}\end{bmatrix} on retrouve donc la règle de dérivation en chaîne :
\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{x}}= \textcolor{orange}{\left( \frac{\text{d} \boldsymbol{u}}{\text{d} \boldsymbol{x}} \right)^\top} \textcolor{blue}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{u}}} Il faut cependant faire attention à l’ordre des termes car le produit matriciel n’est pas commutatif.

Pour la composition avec plusieurs fonctions à valeur vectorielle :

Composition avec deux fonctions vectorielles

f(\boldsymbol{x}) = \textcolor{blue}{\sigma(}\ \textcolor{orange}{\boldsymbol{g}(}\ \textcolor{green}{\boldsymbol{h}(} \boldsymbol{x} \textcolor{green}{)}\ \textcolor{orange}{)}\ \textcolor{blue}{)} = \sigma(\boldsymbol{u}) , \quad \boldsymbol{u}=\boldsymbol{g}( \boldsymbol{v}),\ \boldsymbol{v}=\boldsymbol{h}(\boldsymbol{x}) \Rightarrow \frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{x}} = \left( \textcolor{green}{\frac{\text{d} \boldsymbol{v}}{\text{d} \boldsymbol{x}}} \right)^\top \textcolor{violet}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{v}}} = \left(\textcolor{green}{\frac{\text{d} \boldsymbol{v}}{\text{d} \boldsymbol{x}}} \right)^\top \left( \textcolor{orange}{\frac{\text{d} \boldsymbol{u}}{\text{d} \boldsymbol{v}}} \right)^\top \textcolor{blue}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{u}}} où

\textcolor{green}{\frac{\text{d} \boldsymbol{v}}{\text{d} \boldsymbol{x}}} est la matrice jacobienne de \textcolor{green}{\boldsymbol{h}}
\textcolor{orange}{\frac{\text{d} \boldsymbol{u}}{\text{d} \boldsymbol{v}}} est la matrice jacobienne de \textcolor{orange}{\boldsymbol{g}}

Le nombre d’opérations dans le produit matriciel ci-dessous peut être optimisé en effectuant les calculs dans le bon ordre.

De gauche à droite : O( m n_1 n_2) opérations pour \boldsymbol{Z} =\left(\textcolor{green}{\frac{\text{d} \boldsymbol{v}}{\text{d} \boldsymbol{x}}} \right)^\top \left( \textcolor{orange}{\frac{\text{d} \boldsymbol{u}}{\text{d} \boldsymbol{v}}} \right)^\top, puis O(m n_2) opérations pour \boldsymbol{Z}\textcolor{blue}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{u}}}.
De droite à gauche : O(n_1 n_2) opéartions pour \boldsymbol{z} = \left( \textcolor{orange}{\frac{\text{d} \boldsymbol{u}}{\text{d} \boldsymbol{v}}} \right)^\top \textcolor{blue}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{u}}}, puis O(m n_1) opérations pour \left(\textcolor{green}{\frac{\text{d} \boldsymbol{v}}{\text{d} \boldsymbol{x}}} \right)^\top\boldsymbol{z}.

La rétropropagation du gradient repose sur l’idée d’effectuer les calculs de droite à gauche en mémorisant la plupart des termes : si \boldsymbol{z} =\textcolor{violet}{\frac{\text{d} f(\boldsymbol{x})}{\text{d} \boldsymbol{v}}} a déjà été calculé, uniquement O(m n_1) opérations sont requises.

21.2.3.3 Rétropropagation du gradient dans un réseau de neurones

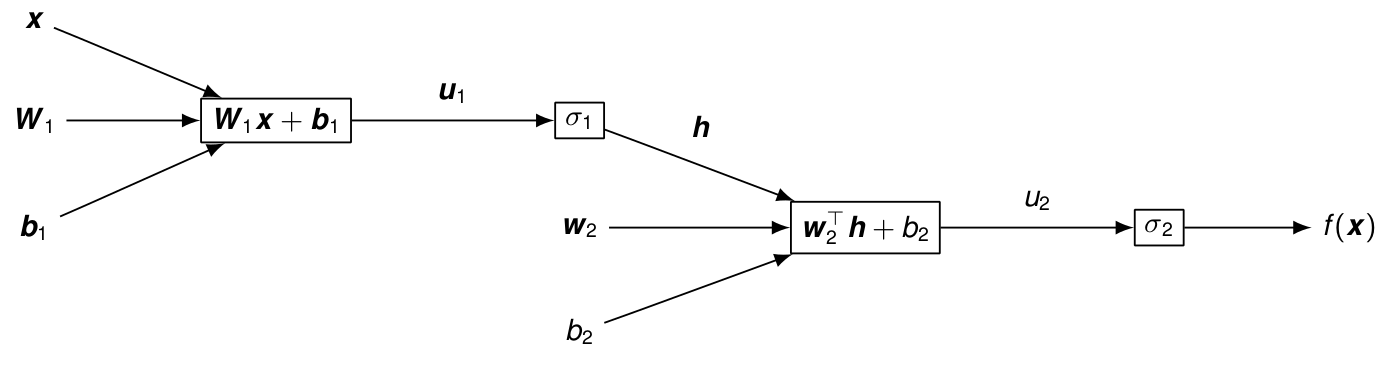
Graphe de calcul pour f(\boldsymbol{x}) = \sigma_2(\ \boldsymbol{w}_2^\top \sigma_1( \boldsymbol{W}_1 \boldsymbol{x} + \boldsymbol{b}_1) + b_2)

\boldsymbol{u}_1 = \boldsymbol{W}_1 \boldsymbol{x} + \boldsymbol{b}_1 = \begin{bmatrix}\boldsymbol{w}_{1,1}^\top \boldsymbol{x} + b_{1,1}\\\vdots\\\boldsymbol{w}_{1,n}^\top \boldsymbol{x} + b_{1,n}\end{bmatrix}, \qquad \boldsymbol{h} = \sigma_1(\boldsymbol{u}_1) = \begin{bmatrix}\sigma_1(u_{1,1})\\\vdots\\\sigma_1(u_{1,n})\end{bmatrix} Les dérivées par rapport aux paramètres de la couche de sortie sont \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{w}_2} = \frac{\partial f(\boldsymbol{x})}{\partial u_2} \frac{\partial u_2}{\partial \boldsymbol{w}_2} = \sigma_2'(u_2)\boldsymbol{h} \quad ; \quad \frac{\partial f(\boldsymbol{x})}{\partial b_2} = \frac{\partial f(\boldsymbol{x})}{\partial u_2} \frac{\partial u_2}{\partial b_2} =\sigma_2'(u_2) Mais pour optimiser ces paramètres avec la descente de gradient stochastique, il faut en fait calculer le gradient de l’erreur en sortie \ell(y,\hat{y}), et donc considérer un graphe de calcul au bout duquel s’ajoute le calcul de l’erreur :

Cela conduit à \frac{\partial \ell(y,\hat{y})}{\partial \boldsymbol{w}_2} = \frac{\partial \ell(y,\hat{y})}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial \boldsymbol{w}_2} = \frac{\partial \ell(y,\hat{y})}{\partial \hat{y}} \sigma_2'(u_2)\boldsymbol{h} \textcolor{red}{\frac{\partial \ell(y,\hat{y})}{\partial b_2}} = \frac{\partial \ell(y,\hat{y})}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial b_2} = \textcolor{red}{\frac{\partial \ell(y,\hat{y})}{\partial \hat{y}} \sigma_2'(u_2)} avec des calculs redondants qui peuvent être économisés si \textcolor{red}{\frac{\partial \ell(y,\hat{y})}{\partial b_2}} est calculé en premier par exemple.

Pour les gradients par rapport aux paramètres de la couche cachée :

le seul chemin de \boldsymbol{w}_{1,k} à f(\boldsymbol{x}) passe uniquement par u_{1,k} et h_k : \textcolor{violet}{\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{w}_{1,k}}} = \textcolor{blue}{\frac{\partial f(\boldsymbol{x})}{\partial u_2}\frac{\partial u_2}{\partial h_k} \frac{\partial h_k}{\partial u_{1,k}}} \textcolor{orange}{ \frac{\partial u_{1,k}}{\partial \boldsymbol{w}_{1,k}} }= \textcolor{blue}{\sigma_2'(u_2) w_{2,k} \sigma_1'(u_{1,k}) } \textcolor{orange}{\boldsymbol{x}} \textcolor{brown}{\frac{\partial f(\boldsymbol{x})}{\partial b_{1,k}}} = \textcolor{blue}{\frac{\partial f(\boldsymbol{x})}{\partial u_2}\frac{\partial u_2}{\partial h_k} \frac{\partial h_k}{\partial u_{1,k}} } \textcolor{orange}{\frac{\partial u_{1,k}}{\partial b_{1,k}} } = \textcolor{blue}{\sigma_2'(u_2) w_{2,k} \sigma_1'(u_{1,k})} Et pour l’erreur en sortie \ell(y,\hat{y}) : \begin{align*} \frac{\partial \ell(y,\hat{y})}{\partial b_{1,k}} &= \textcolor{green}{ \frac{\partial \ell(y,\hat{y})}{\partial \hat{y}} } \textcolor{brown}{\frac{\partial \hat{y}}{\partial b_{1,k}}} = \textcolor{green}{\frac{\partial \ell(y,\hat{y})}{\partial \hat{y}}} \textcolor{blue}{\sigma_2'(u_2) w_{2,k} \sigma_1'(u_{1,k})}\\ \frac{\partial \ell(y,\hat{y})}{\partial \boldsymbol{w}_{1,k}} &= \textcolor{green}{\frac{\partial \ell(y,\hat{y})}{\partial \hat{y}} }\textcolor{violet}{\frac{\partial \hat{y}}{\partial \boldsymbol{w}_{1,k}}} =\textcolor{green}{\frac{\partial \ell(y,\hat{y})}{\partial \hat{y}}} \textcolor{blue}{\sigma_2'(u_2) w_{2,k} \sigma_1'(u_{1,k})}\textcolor{orange}{ \boldsymbol{x}} \end{align*} Ici encore, on peut remarquer que \textcolor{red}{\frac{\partial \ell(y,\hat{y})}{\partial \hat{y}}\sigma_2'(u_2)} a déjà été calculé dans \textcolor{red}{\frac{\partial \ell(y,\hat{y})}{\partial b_{2}}} au niveau de la couche supérieure. C’est toute l’idée de la rétropropagation qui consiste à calculer les gradients en propageant l’information de la sorite vers l’entrée du réseau.

Résumé de l’algorithme de rétropropagation du gradient

On utilise la descente de gradient stochastique : de petites itérations qui minimisent l’erreur en sortie \ell(y_i, f(\boldsymbol{x}_i)) sur 1 exemple.
Chaque itération demande le calcul du gradient de l’erreur par rapport aux paramètres.
Les gradients peuvent être calculés en (retro)propageant l’information de la sortie vers l’entrée pour économiser énormément de calculs.

Donc, on boucle sur les étapes suivantes :

tirer un exemple (\boldsymbol{x}_i, y_i) ;
calculer f(\boldsymbol{x}_i) en mémorisant toutes les quantités intermédiaires (\boldsymbol{u}_1, \boldsymbol{h}, u_2, … ) (forward pass) ;
calculer récursivement les gradients \frac{\text{d} \ell(y_i, f(\boldsymbol{x}_i))}{\text{d} \boldsymbol{w}} pour tous les paramètres \boldsymbol{w} (backward pass) ;
mettre à jour \boldsymbol{w} \leftarrow \boldsymbol{w} - \mu \frac{\text{d} \ell(y_i, f(\boldsymbol{x}_i))}{\text{d} \boldsymbol{w}}.

Et l’algorithme fait plusieurs passages ainsi à travers la base d’apprentissage. Chaque passage sur l’ensemble de la base s’appelle une époque (ou epoch).

21.2.4 Variantes de l’algorithme

En pratique, on utilise plutôt des « mini-batch » aléatoires I\subset\{1,\dots m\} (|I|\approx 10 ou 100) pour optimiser chaque itération sur un petit ensemble de points au lieu d’un seul point : \boldsymbol{w} \leftarrow \boldsymbol{w} - \mu \frac{1}{|I|}\sum_{i\in I} \frac{\text{d} \ell(y_i, f(\boldsymbol{x}_i))}{\text{d} \boldsymbol{w}}

La taux d’apprentissage \mu peut aussi être modifié au cours de l’apprentissage, typiquement pour démarrer avec une grande valeur \mu_0 qui décroît au cours du temps 0\leq t\leq\tau jusqu’à \mu_{\tau} : \mu\leftarrow (1-\frac{t}{\tau})\mu_0 + \frac{t}{\tau}\mu_{\tau}

On peut aussi ajouter de l’inertie dans les mises à jour (du « momentum ») avec \alpha\in[0,1) : \boldsymbol{v} \leftarrow \alpha \boldsymbol{v} - \mu \frac{1}{|I|}\sum_{i\in I} \frac{\text{d} \ell(y_i, f(\boldsymbol{x}_i))}{\text{d} \boldsymbol{w}} \boldsymbol{w} \leftarrow \boldsymbol{w} + \boldsymbol{v} Cela permet de limiter les oscillations contraires entre les mises à jour successives.

En résumé, il existe beaucoup d’heuristiques différentes pour adapter \mu ou implémenter l’inertie telles que AdaGrad, RMSprop, Adam…

21.3 Réseaux de neurones pour la classification

Pour la régression, l’algorithme ci-dessus s’applique directement à la fonction de perte quadratique. Mais pour la classification, la perte 0-1 n’est pas dérivable et ne peut donc pas être utilisée directement.

À la place, nous utilisons un encodage 0-1 des étiquettes : par exemple pour C=3 catégories, \boldsymbol{y} = \begin{bmatrix}1\\0\\0\end{bmatrix},\ si\ y = 1,\quad \boldsymbol{y} = \begin{bmatrix}0\\1\\0\end{bmatrix},\ si\ y = 2,\quad \boldsymbol{y} = \begin{bmatrix}0\\0\\1\end{bmatrix},\ si\ y = 3 et nous construisons un réseau à C sorties, ou à sortie vectorielle \hat{\boldsymbol{y}} = \boldsymbol{f}(\boldsymbol{x}) = \begin{bmatrix}\hat{y}_1\\\hat{y}_2\\\hat{y}_3\end{bmatrix}= \mathbf{softmax}(\boldsymbol{u}) avec \boldsymbol{u}\in\mathbb{R}^C contenant un score réel pour chaque catégorie et \hat{y}_k = \mathbf{softmax}_k(\boldsymbol{u}) = \frac{e^{u_k}}{\sum_{j=1}^Q e^{u_j}} La fonction softmax permet de garantir que les sorties \hat{y}_k sont dans [0,1] et normalisées telles que \sum_{k=1}^Q \hat{y}_k = 1. Ainsi, elles estiment l’encodage 0-1 \boldsymbol{y} et peuvent être interprétées comme une loi de probabilité discrète sur les catégories : \hat{y}_k = \widehat{P}(Y=k|X=x).

La catégorie prédite est ensuite donnée par la probabilité maximale : \arg\max_{k\in\{1,\dots,C\}} \hat{y}_k

Dans ce cas, l’apprentissage se fait typiquement en minimisant l’entropie croisée : \ell(\boldsymbol{y},\hat{\boldsymbol{y}}) = -\sum_{k=1}^Q y_k \log \hat{y}_k = -\log \hat{y}_{y} sachant que minimiser \ell(\boldsymbol{y},\hat{\boldsymbol{y}}) revient à maximiser \hat{y}_{y} = \widehat{P}(Y=y|X=x).

Le calcul des dérivées s’effectue ainsi : avec \ell(\boldsymbol{y},\hat{\boldsymbol{y}}) =-\log \hat{y}_{y} = -u_y + \log \sum_{j=1}^Q e^{u_j} on a \frac{\partial \ell(\boldsymbol{y},\hat{\boldsymbol{y}})}{\partial u_k} = - \mathbf{1}(k=y) + \frac{e^{u_k}}{\sum_{j=1}^Q e^{u_j}} = \hat{y}_k - \mathbf{1}(k=y) = \hat{y}_k - y_k et donc \frac{\partial \ell(\boldsymbol{y},\hat{\boldsymbol{y}})}{\partial u_k} \begin{cases} \leq 0 ,& si\ k=y\\ \geq 0,& si\ k\neq y\\ = 0,& si \ \hat{y}_k=\mathbf{1}(k=y) \end{cases} (où le dernier cas pour \hat{y}_k=\mathbf{1}(k=y) ne peut jamais arriver).