7 Estimation du risque
En apprentissage, le risque (ou erreur de généralisation) d’un modèle de prédiction est défini comme l’espérance de la fonction de perte : R(f) = \mathbb{E}\ell(f, \boldsymbol{X}, Y) et n’est pas calculable en pratique sans la connaissance de la loi de probabilité du couple (\boldsymbol{X},Y) ni l’accès à une infinité d’exemples (tirages de (\boldsymbol{X},Y)).
À partir des données de la base d’apprentissage S = \left((\boldsymbol{x}_i, y_i)\right)_{1\leq i\leq m}, nous pouvons calculer le risque empirique R_{emp}(f) = \frac{1}{m} \sum_{i=1}^{m} \ell(f, \boldsymbol{x}_i,y_i) mais celui-ci ne permet pas d’estimer R(f) correctement lorsque le modèle f dépend des données (x_i, y_i) elles-mêmes (notamment à cause du surapprentissage). Il est donc nécessaire de disposer d’autres techniques pour estimer les performances des modèles de prédiction.
7.1 Erreur de test
Une approche assez simple consiste à conserver de côté une partie des données pour créer une base de test avec des données indépendantes de la base d’apprentissage :
S_{test} = \left((\boldsymbol{x}_i', y_i')\right)_{1\leq i\leq m_{test}}
sur laquelle nous pouvons calculer l’erreur de test
R_{test}(f) = \frac{1}{m_{test}} \sum_{i=1}^{m_{test}} \ell(f, \boldsymbol{x}_i',y_i')
Pour rester valide, l’erreur de test doit bien être calculée sur des données indépendantes des données d’apprentissage, mais aussi du modèle f et donc de toute la procédure de sélection de ce modèle.
La base de test ne peut donc pas être utilisée pour régler les hyperparamètres de l’algorithme.
7.1.1 Quelles garanties sur les performances en généralisation ?
Il est possible de garantir les performances en généralisation à partir de l’erreur de test.
Pour tout classifieur f et tout \delta>0, avec une probabilité égale ou supérieure à 1-\delta sur le tirage aléatoire de la base de test, R(f) \leq R_{test}(f) + \sqrt{\frac{\ln\frac{1}{\delta}}{2m_{test}}} \tag{7.1} Cette borne nous dit que le véritable risque R(f) est estimé avec une précision de \epsilon=\sqrt{\frac{\ln\frac{1}{\delta}}{2m_{test}}} par l’erreur de test R_{test}(f).
Attention : cette borne n’est valide qu’avec une forte probabilité définie par l’indice de confiance \delta. Le risque reste une quantité inaccessible avec une certitude de 100%. Cependant, il est tout à fait possible d’être assez sûr de ce que l’on avance à partir de l’erreur de test.
Pour obtenir cette garantie, nous utilisons l’inégalité de Hoeffding :
Soit n variables aléatoires, Z_1,\dots,Z_n, indépendantes et identiquement distribuées selon la loi de Z, et une fonction bornée h telle que h(Z) \in [a,b]. Alors, pour tout \epsilon> 0, P\left\{\mathbb{E}[h(Z)] - \frac{1}{n}\sum_{i=1}^n h(Z_i) \geq \epsilon \right\} \leq \exp\left(\frac{-2n\epsilon^2}{(b-a)^2}\right)
qui est instanciée avec
- un couple aléatoire exemple/étiquette Z = (X,Y) ;
- un échantillon (Z_i)_{1\leq i\leq n} = (X'_i,Y'_i)_{1\leq i\leq m_{test}} de n=m_{test} copies indépendantes de Z
- une fonction de perte de classification h(Z) = \mathbf{1}(f(X)\neq Y) bornée avec a=0 et b=1
Cela nous donne P\left\{R(f) - R_{test}(f) \geq \epsilon \right\} \leq \exp\left(-2m_{test}\epsilon^2\right) qui peut être utilisé ainsi : \begin{align*} P \left\{R(f) \leq R_{test}(f) + \epsilon \right\} &= 1 - P \left\{R(f) > R_{test}(f) + \epsilon \right\} \\ &\leq 1 - P \left\{R(f) \geq R_{test}(f) + \epsilon \right\} \\ &\leq 1 - \exp\left(-2m_{test}\epsilon^2\right) \end{align*} En posant \delta = \exp\left(-2m_{test}\epsilon^2\right) cela donne \epsilon=\sqrt{\frac{\ln\frac{1}{\delta}}{2m_{test}}} et la garantie d’avoir un écart pus faible que ce \epsilon entre le risque et l’erreur de test avec une probabilité d’au moints 1-\delta.
7.1.2 Combien d’exemples faut-il dans la base de test pour garantir une bonne estimation de R(f) ?
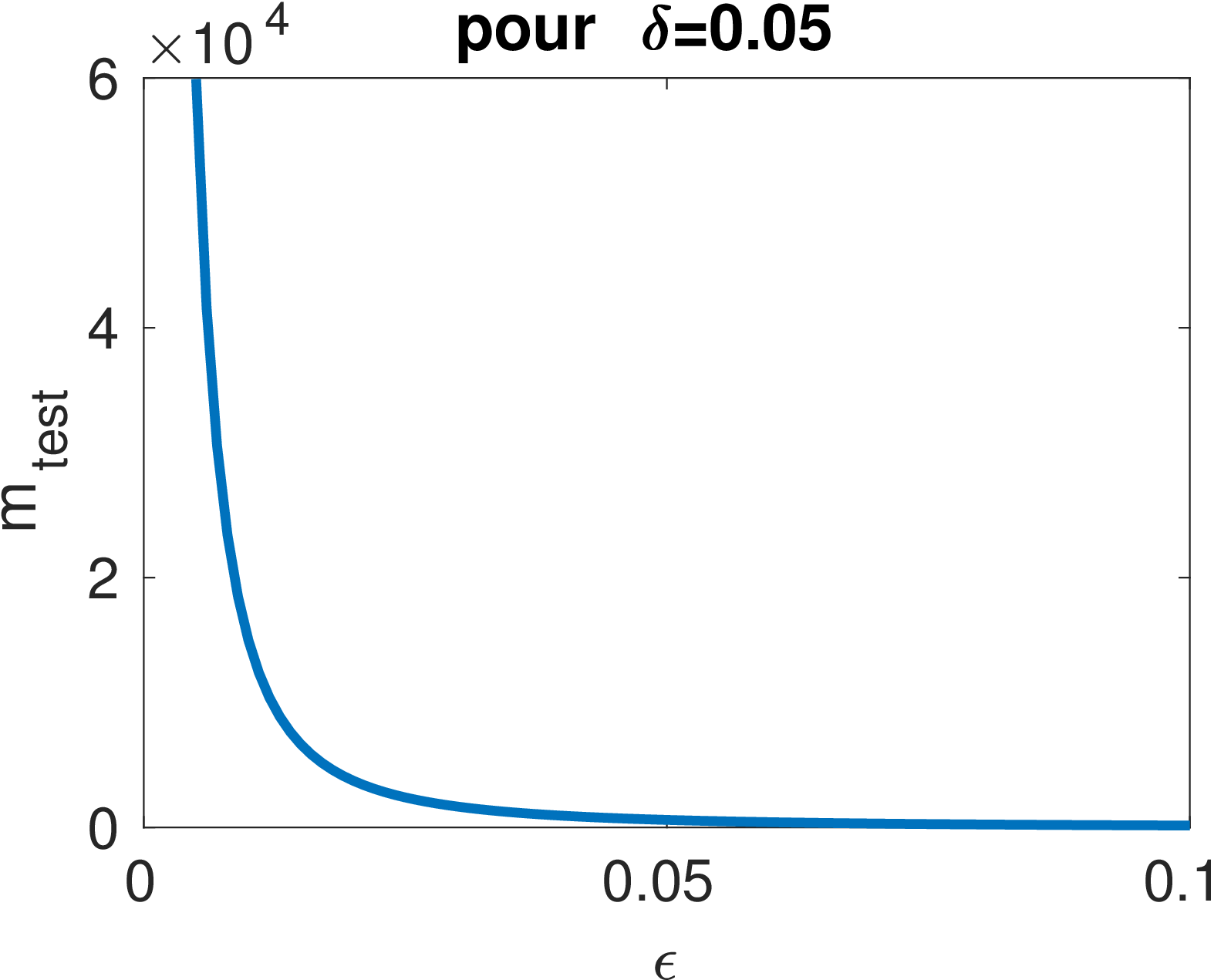
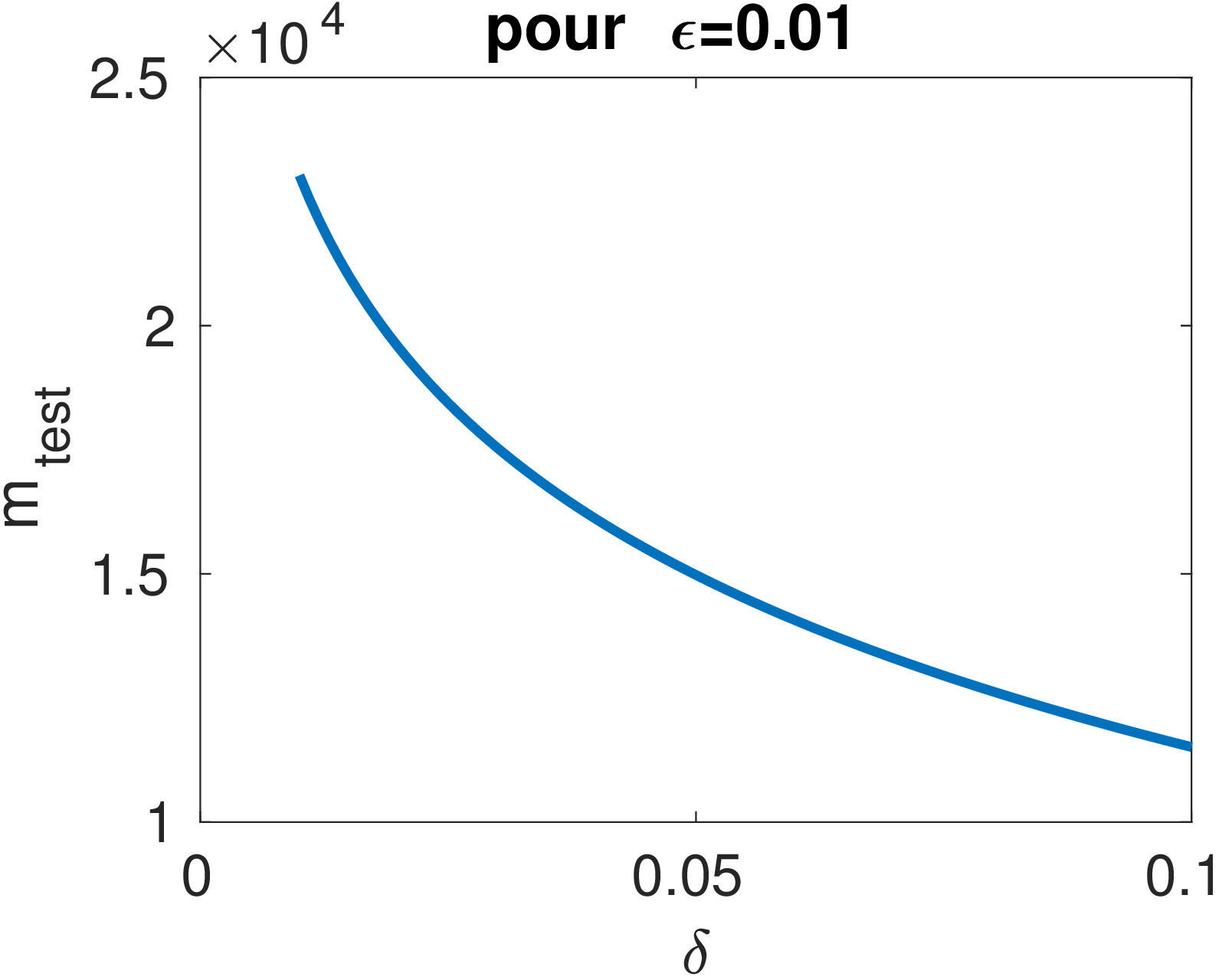
Pour une précision \epsilon souhaitée et un indice de confiance \delta fixé, la borne R(f) \leq R_{test}(f) + \epsilon est satisfaite avec une probabilité d’au moins 1-\delta si m_{test}\geq \frac{\ln \frac{1}{\delta}}{2\epsilon^2} Pour obtenir ce résultat, il suffit de résoudre \delta = \exp\left(-2m_{test}\epsilon^2\right) par rapport à m au lieu de \epsilon.
Les courbes ci-dessous permettent de visualiser l’influence de \epsilon et \delta sur le nombre d’exemples de test nécessaire.
Par exemple, pour garantir une précision de \epsilon=1\% avec une confiance de 95\% (\delta = 0.05), on doit avoir m_{test}\geq 14980.
7.1.3 Que gagne-t-on à avoir une plus grande base de test ?
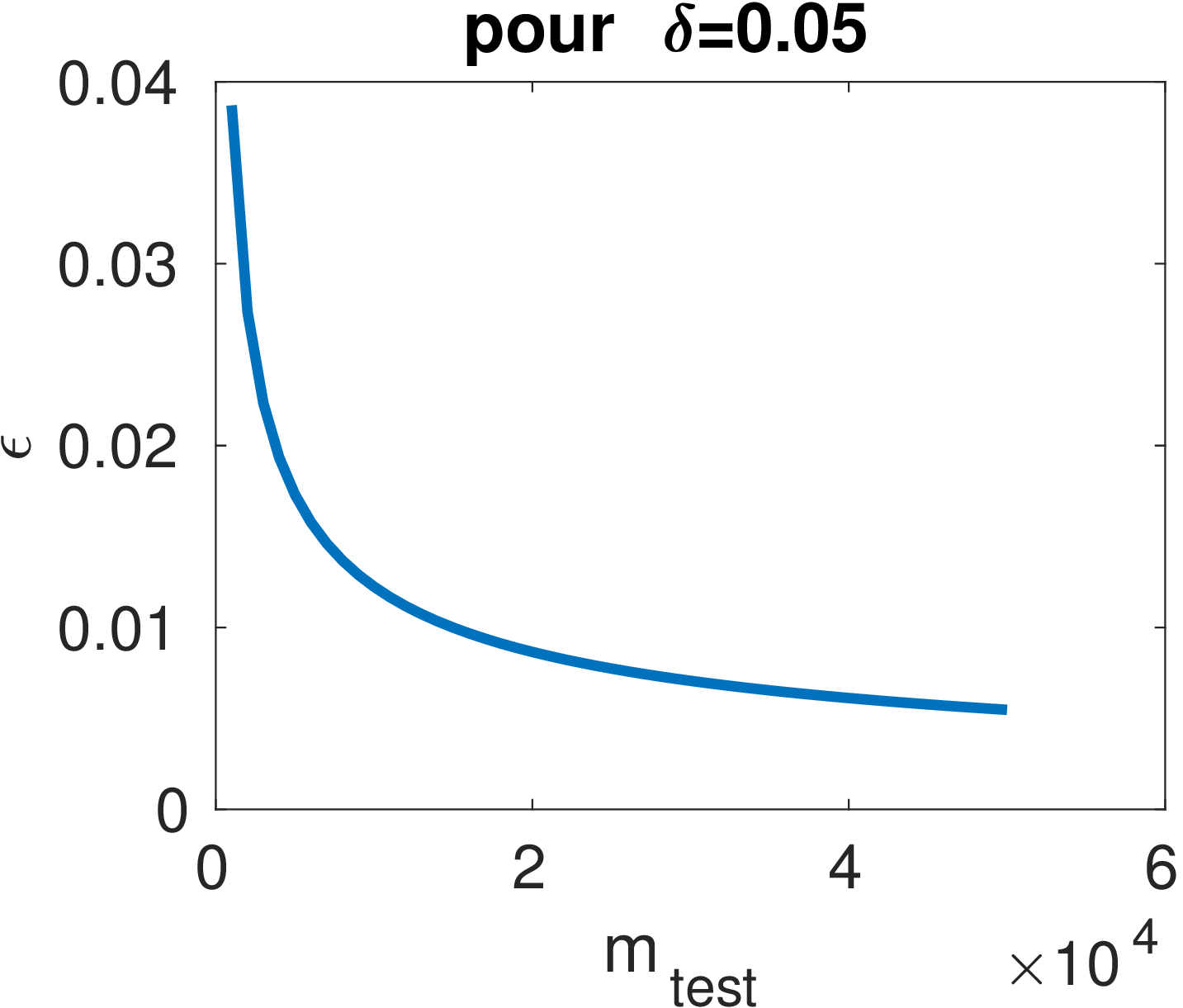
La courbe ci-dessous montre la précision de l’estimation à partir de l’erreur de test en fonction de la taille de la base de test.
On peut voir notamment qu’il n’est pas très intéressant d’avoir de très grandes bases de test car le gain en termes de précision n’est pas très important après m>50\ 000.
7.1.4 Applicabilité de ces courbes et de la borne Équation 7.1
Les résultats ci-dessus sont valables
- quel que soit le problème / la distribution des données,
- quel que soit le classifieur / l’algorithme choisi,
sous l’hypothèse d’une base de test indépendante contenant des exemples indépendants et identiquement distribués.
Une autre limite concerne le choix de la fonction de perte utilisée pour calculer le risque. Les résultats sont limités à la classification avec l’erreur 0-1.
Cependant, en régression, il est possible d’obtenir le même type de résultats. La seule différence concerne l’amplitude de l’erreur donnée par a et b dans l’inégalité de Hoeffding. Pour \ell(f,\boldsymbol{X}, Y) = (Y - f(\boldsymbol{X}))^2, si les sorties sont bornées, Y\in[-M, M], et que les modèles le sont aussi, f(\boldsymbol{X})\in[-M,M], alors \ell(f,\boldsymbol{X}, Y) \in[0, 4M^2] et la garantie devient :
Pour tout \delta>0, avec une probabilité égale ou supérieure à 1-\delta sur le tirage aléatoire de la base de test, R(f) \leq R_{test}(f) + 4M^2 \sqrt{\frac{\ln\frac{1}{\delta}}{2m_{test}}} \tag{7.2} c’est-à-dire que \epsilon est simplement multiplié par l’amplitude maximale de l’erreur (le \epsilon précédent peut donc être vu comme un pourcentage de cette amplitude).
7.2 Validation croisée
L’erreur de test est un bon estimateur du risque, mais il a un défaut notoire : il nécessite de mettre des données de côté qui ne sont plus disponibles pour l’apprentissage. Lorsque que les données sont trop peu nombreuses, cela n’est pas toujours raisonable car l’algorithme n’a plus assez d’exemples pour apprendre correctement.
La validation croisée permet de palier à ce problème avec une procédure itérative qui considère un jeu de test différent à chaque itération.
7.2.1 K-fold
La procédure K-fold est basée sur le découpage de l’ensemble des données en K paquets. Puis, à chaque itération un paquet différent est sélectionné pour le test et les K-1 paquets restants servent à l’apprentissage.
Par exemple, pour K=5, cela donne les 5 itérations suivantes :
| Itération | Paquet 1 | Paquet 2 | Paquet 3 | Paquet 4 | Paquet 5 | Erreur |
|---|---|---|---|---|---|---|
| 1 | Test | App | ren | tis | sage | R_1 |
| 2 | App | Test | ren | tis | sage | R_2 |
| 3 | App | ren | Test | tis | sage | R_3 |
| 4 | App | ren | tis | Test | sage | R_4 |
| 5 | App | ren | tis | sage | Test | R_5 |
À la fin de la procédure, le risque du modèle f appris sur toutes les données est estimé par R_{Kfold}(f) = \frac{1}{K}\sum_{k=1}^K R_k où R_k est l’erreur moyenne calculée sur le paquet de Test du modèle appris à la même itération sur les K-1 autres paquets.
7.2.2 Leave-one-out (LOO)
L’estimateur du risque LOO est donné par R_{loo}(\hat{f}_S) = \frac{1}{m}\sum_{i=1}^m \ell(\hat{f}_{S\setminus (\boldsymbol{x}_i,y_i)}, \boldsymbol{x}_i,y_i) où \hat{f}_S est le modèle appris sur la base S.
Le LOO correspond simplement au cas limite du K-fold avec K=m : chaque exemple forme un « paquet » et il y autant d’itérations que de données disponibles.
Cette procédure est bien plus coûteuse en temps, car il faut réaliser m apprentissage, mais elle est parfois nécessaire lorsque m est trop faible.
Le LOO est un estimateur « presque non biaisé » du risque : \mathbb{E}_S R_{loo}(\hat{f}_S) = \mathbb{E}_{S'} R(\hat{f}_{S'}) pour des jeux de données aléatoires S de m exemples et S' de m-1 exemples.
\begin{align*} \mathbb{E}_S R_{loo}(\hat{f}_S) &= \frac{1}{m}\sum_{i=1}^m \mathbb{E}_S \ell(\hat{f}_{S\setminus (X_i,Y_i)}, X_i,Y_i)& (\mathbb{E}\text{ est linéaire})\\ &= \frac{1}{m}\sum_{i=1}^m \mathbb{E}_S \ell(\hat{f}_{S\setminus (X_1,Y_1)}, X_1,Y_1) & (car\ S\ est\ iid)\\ &= \mathbb{E}_S \ell(\hat{f}_{S\setminus (X_1,Y_1)}, X_1,Y_1)% & (car\ \E_S \ell(\hat{f}_{S\setminus (X_1,Y_1)}, X_1,Y_1)\\\ est\ constant) \\ \\& = \mathbb{E}_{S', (X_1,Y_1)} \ell(\hat{f}_{S'}, X_1,Y_1) \\ &= \mathbb{E}_{S'} \mathbb{E}_{(X_1,Y_1)} \ell(\hat{f}_{S'}, X_1,Y_1) & (car\ (X_1,Y_1)\text{ est indép.\ de}\ S') \\ &= \mathbb{E}_{S'} R(\hat{f}_{S'}) \end{align*}