1 Résolution de problèmes

Nous présentons ici les algorithmes d’intelligence artificielle dédiés à la résolution de problèmes. Il s’agit ici de développer des « agents intelligents », au sens où ceux-ci devraient être capables d’agir de manière rationnelle.

Un agent

vie/évolue dans un environnement
perçoit son environnement grâce à ses capteurs
agit sur cet environnement grâce à des actionneurs/effecteurs.

Un agent intelligent est un agent qui exécute la meilleure action possible étant donné sa perception du monde.

Dans cette définition, il faut bien faire la différence entre l’agent intelligent et l’omniscient. On ne demande pas à l’agent de prendre la meilleure décision dans l’absolu, mais uniquement la meilleure à la vue de ce qu’il a pu observé du monde.

1.1 Formalisation d’un problème

Avant de pouvoir appliquer un algorithme de résolution de problème, il faut commencer par formaliser le problème. Cela se fait avec les composants suivants :

un objectif que l’on cherche atteindre ;
une liste d’actions possibles ;
une définition de l’état du monde dans lequel l’agent évolue (la concaténation des variables qui représentent ce monde) ;
l’état initial au début de la réflexion ;
une fonction de transition qui définit l’état dans lequel le monde se retrouve après avoir pris telle action dans tel état ;
(éventuellement) le coût de chaque action.

A partir de ces éléments, on définit également le but qui est l’ensemble des états dans lesquels l’objectif est atteint.

Les algorithmes de résolution de problèmes recherchent donc une solution qui est une suite d’actions garantissant d’atteindre le but à partir de l’état initial. Il peut exister plusieurs solutions pour le même problème, et dans ce cas on cherchera à obtenir si possible une solution de coût minimal.

1.2 Arbre de recherche

Les algorithmes de recherche pour la résolution de problèmes sont basés sur l’exploration d’un arbre de recherche dont les éléments ont la signification suivante :

chaque nœud contient un état du problème ;
chaque branche correspond à une action possible à partir de cet état (éventuellement pondérée par le coût de l’action) ;
la racine contient l’état initial.

Une solution du problème est un chemin correspondant à une séquence d’actions qui mène de la racine jusqu’à un nœud dont l’état appartient au but. Le coût d’une solution est la somme des pondérations des branches traversées par le chemin.

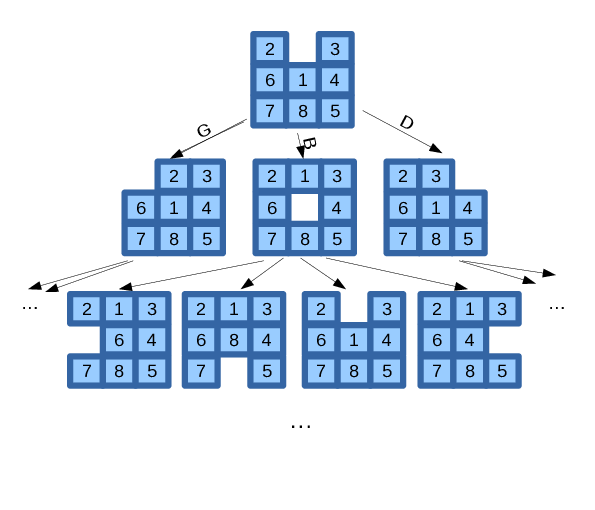
1.3 Exemple : le taquin

état : position des pièces et du trou ;
actions possibles : déplacer le trou vers le haut, le bas, la gauche ou la droite (en fonction de l’état, certaines actions sont impossibles) ;
coût d’une action = 1 pour toutes les actions car on cherche à minimiser le nombre de coups pour arriver au but.

Arbre de recherche :

1.4 Algorithmes de recherche « aveugles »

Tous les algorithmes de recherche explorent l’arbre de recherche dans des directions différentes et s’arrêtent dès qu’ils trouvent un nœud dont l’état appartient au but et retourne la solution correspondant au chemin de la racine à ce nœud.

1.4.1 Recherche en Largeur d’abord

Dans une recherche en largeur d’abord, l’arbre est exploré couche par couche en partant de la racine.

Cela garantie de trouver une solution avec le moins d’actions possibles mais demande beaucoup de mémoire. En effet, pour pouvoir explorer couche par couche, il faut au minimum retenir l’équivalent d’une couche en mémoire.

Si n est la longueur de la solution la plus courte (en nombre d’actions), alors l’arbre construit sera de profondeur n. Et si le facteur de branchement (le nombre de fils de chaque nœud) est b, alors le nombre de nœuds sur la dernière couche est b^n. Si b\geq 10 et que la solution est de longueur n\geq 12, alors la taille de cette couche dans la mémoire est de l’ordre du Teraoctet.

1.4.2 Recherche en Profondeur d’abord

Dans la recherche en profondeur d’abord, chaque branche est explorée jusqu’à la profondeur maximale avant de passer à la branche suivante, qui correspond à la plus profonde non encore explorée.

Cette recherche est plus efficace en termes de mémoire, car il suffit de retenir la branche courante en mémoire. Pour une profondeur n et un facteur de branchement b, la taille de cette branche est de l’ordre de bn, donc bien inférieur à b^n.

La recherche en profondeur d’abord peut trouver une solution rapidement si elle se trouve dans une des premières branches explorées, mais elle peut aussi perdre beaucoup de temps dans des branches inintéressantes.

En pratique, il est aussi utile d’altérer la liste des actions possibles pour éviter les cycles qui conduisent à creuser une branche de profondeur infinie en tournant en rond.

1.4.3 Recherche mixte/en profondeur d’abord itérée

La recherche en profondeur d’abord itérée permet de bénéficier des avantages des deux recherches précédentes. L’idée est d’appliquer la recherche en profondeur d’abord en incrémentant progressivement la profondeur maximale autorisée.

Ainsi, toute la couche de profondeur 1 est explorée avant celle à la profondeur 2 et ainsi de suite, selon le même ordre quand dans une recherche en largeur d’abord, ce qui conduit aux mêmes garanties de trouver la solution la plus courte.

L’avantage ici est que le cœur de l’algorithme fonctionne en profondeur d’abord et ne nécessite de retenir en mémoire que la branche courante. Le prix à payer pour bénéficier de tous ces avantages se compte en temps de calcul : pour explorer la couche à la profondeur n, l’algorithme repart de la racine et doit repasser par toutes les couches précédentes.

1.4.4 Recherche à Coût uniforme

La recherche en largeur d’abord donne des garanties uniquement en termes du nombre d’actions. Mais la solution la plus courte en actions n’est pas nécessairement la meilleure au sens du coût.

La recherche à coût uniforme explore à chaque itération le nœud qui minimise le coût g(nœud) entre la racine et le nœud.

Ainsi, lorsqu’elle trouve une solution, elle garantie qu’aucune autre solution ne possède un coût plus faible.

Si cette recherche est appliquée avec un coût constant pour chaque action (comme pour le taquin), alors le résusltat sera identique à la recherche en largeur d’abord.

1.5 Algorithmes de recherche « informés »

Les algorithmes de recherche informés incluent de la connaissance sur le problème au travers d’une fonction heuristique h(noeud) qui estime le coût restant pour le meilleur chemin entre le nœud et le but. Cette heuristique est utilisée afin d’explorer le nœud qui paraît être le « meilleur » d’abord.

1.5.1 Recherche gloutonne

La recherche gloutonne explore le nœud qui minimise h(noeud) pour se rapprocher le plus possible du but, mais sans garantie sur le coût de la solution car l’heuristique n’est qu’une estimation du coût réel.

1.5.2 A*

L’algorithme A* combine le coût uniforme et la recherche gloutonne pour explorer le nœud qui minimise f(noeud) = g(noeud) + h(noeud) = estimation du coût total d’une solution passant par noeud.

Si l’heuristique est admissible (elle ne surestime jamais le coût total d’une solution passant par noeud), alors l’algorithme A* est optimal : il retourne une solution qui minimise le coût.

1.6 Algorithme générique

Tous les algorithmes ci-dessus peuvent être implémentés à partir d’un squelette identique :

Initialiser la file d’attente avec la racine.
Prendre un nœud dans la file d’attente.
Vérifier si le but est atteint à ce nœud (si oui, retourner la solution).
Développer le nœud et ajouter les fils à la file d’attente.
Retourner à l’étape 2.

La seule différence entre tous les algorithmes ci-dessus réside dans la manière d’ordonner la file d’attente :

Largeur d’abord : ajouter les nouveaux nœud à la fin de la file
Coût uniforme : trier la file par ordre croissant de g(noeud)
Profondeur d’abord : ajouter les nouveaux nœuds au début de la file
Glouton : trier la file par ordre croissant de h(noeud)
A* : trier la file par ordre croissant de f(noeud) = g(noeud) + h(noeud)