4 Réseaux bayésiens

Les réseaux bayésiens permettent de modéliser des phénomènes aléatoires complexes impliquant de nombreuses variables aléatoires par une approche graphique mettant en valeur les dépendances entre variables et limitant la taille de la représentation.

4.1 Représetation directe d’une loi jointe

Un vecteur aléatoire \boldsymbol{X}\in\mathbb{R}^n est la concaténation de n variables aléatoires. Leur loi jointe se définie comme pour un couple de variables aléatoires. En particulier, pour un vecteur aléatoire discret : P(\boldsymbol{X} = \boldsymbol{x}) = P(X_1 = x_1, X_2=x_2,\dots, X_n = x_n) la loi jointe donne la probabilité d’observer les valeurs x_1,...,x_n pour les toutes les composantes X_1,...,X_n de \boldsymbol{X}.

Si l’on se limite à des vecteurs binaires \boldsymbol{X}\in\{0,1\}^n, alors il est possible de représenter cette loi de probabilité par un tableau

Table 4.1: Représentation de la loi joint par un tableau de probabilités

x_1	x_2	x_n	P(\boldsymbol{X}=(x_1,x_2,\dots,x_n) )
0	0	0	0.1
0	0	1	0.3
	\vdots		\vdots

Mais la taille de ce tableau peut vite rendre cette approche directe irréalisable. En considérant que les valeurs des x_i encodent l’indice de la ligne en binaire, il ne reste que la dernière colonne à stocker dans la mémoire, mais cela représente 2^n cases de nombres réels. Si l’on considère des double encodés sur 8 octets, cela donne les tailles de tableau suivantes :

n	taille mémoire du tableau
10	8 Ko
20	8 Mo
30	8 Go
40	8 To

Très vite, ce tableau ne tient plus en mémoire, ni même sur un disque dur.

En réalité, il suffit de ne stocker que 2^n-1 valeurs car la somme de toutes les probabilités doit être égale à 1 et il est donc possible de calculer la valeur non stockée comme 1 moins la somme des autres. Cependant, cela ne change pas vraiment le problème (et est probablement une mauvaise idée à implémenter en pratique).

Important

La Table 4.1 a un autre gros défaut : la plupart des valeurs de la loi jointe sont inconnues ou difficiles à estimer car elles impliquent des cas de figures que l’expert du système modélisé n’a (presque) jamais rencontré. Et ces cas sont en si grand nombre qu’il est difficile de tous les considérer.

4.2 Représentation graphique d’une loi jointe

Un réseau bayésien représente une loi jointe de n variables avec un graphe orienté sans cycles tel que :

chaque nœud correspond à une variable aléatoire (v.a.) ;
les arcs orientés déterminent les (in)dépendances conditionnelles entre variables de sorte que chaque v.a. est conditionnellement indépendante de ses prédécesseurs sachant ses parents : P(X_i = x_i | \boldsymbol{X}_{1:i-1} =\boldsymbol{x}_{1:i-1}) = P(X_i = x_i | \boldsymbol{X}_{parents(X_i)} = \boldsymbol{x}_{parents(X_i)}) où \boldsymbol{X}_{1:i} = (X_1, X_2, \dots, X_i), parents(X_i) est l’ensemble des parents de X_i et les v.a. sont ordonnées de telles que j\in parents(X_i) \Rightarrow j < i,

4.2.1 Factorisation de la loi jointe

Les règles de construction du graphe permettent d’obtenir la factorisation de la jointe P(\boldsymbol{X} = \boldsymbol{x}) = \prod_{i=1}^n P(X_i = x_i\ |\ \boldsymbol{X}_{parents(X_i)} = \boldsymbol{x}_{parents(X_i)}) \tag{4.1} qui constitue la définition de base d’un réseau bayésien.

Preuve

En utilisant la factorisation de la loi d’un couple récursivement, nous avons \begin{align*} P(\boldsymbol{X} = \boldsymbol{x}) &= P(X_n= x_n | \boldsymbol{X}_{1:n-1} = \boldsymbol{x}_{1:n-1} ) P( \boldsymbol{X}_{1:n-1} = \boldsymbol{x}_{1:n-1} ) \\ &= P(X_n= x_n | \boldsymbol{X}_{1:n-1} = \boldsymbol{x}_{1:n-1} ) P(X_{n-1}= x_{n-1} | \boldsymbol{X}_{1:n-2} = \boldsymbol{x}_{1:n-2}) P( \boldsymbol{X}_{1:n-2} = \boldsymbol{x}_{1:n-2} ) \\ &=\dots\\ &= \prod_{i=1}^n P(X_i = x_i | \boldsymbol{X}_{1:i-1} =\boldsymbol{x}_{1:i-1} ) = \prod_{i=1}^n P(X_i = x_i | \boldsymbol{X}_{parents(X_i)} = \boldsymbol{x}_{parents(X_i)} ) \end{align*} avec {1:0} = \emptyset et parents(X_1)= \emptyset.

4.2.2 Tables de probabilités conditionnelles

D’après la factorisation Équation 4.1, il suffit donc de connaître les valeurs des probabilités conditionnelles P(X_i = x_i\ |\ \boldsymbol{X}_{parents(X_i)} = \boldsymbol{x}_{parents(X_i)}) pour pouvoir calculer n’importe quelle probabilité P(\boldsymbol{X}=\boldsymbol{x}) sans avoir besoin de stocker toute la Table 4.1.

Pour des variables discrètes, cela revient à stocker les tables de probabilités conditionnelles associées à chaque variable X_i.

En plus du gain mémoire, les valeurs de ces probabilités conditionnelles correspondent à des quantitées beaucoup plus simples à connaître ou estimer, ce qui permet en général de résoudre le problème identifié ici.

Exemple d’un réseau en forme de chaîne

Dans ce réseau, 5 nombres suffisent pour encoder la loi jointe de 3 variables binaires au lieu de 2^3-1 = 7. On peut calculer par exemple \begin{align*}P(A=0,B=1,C=1) &= P(C=1 | B = 1) P(B=1 | A=0) P(A=0) \\&= 0.9\times 0.2\times 0.8 = 0.144\end{align*}

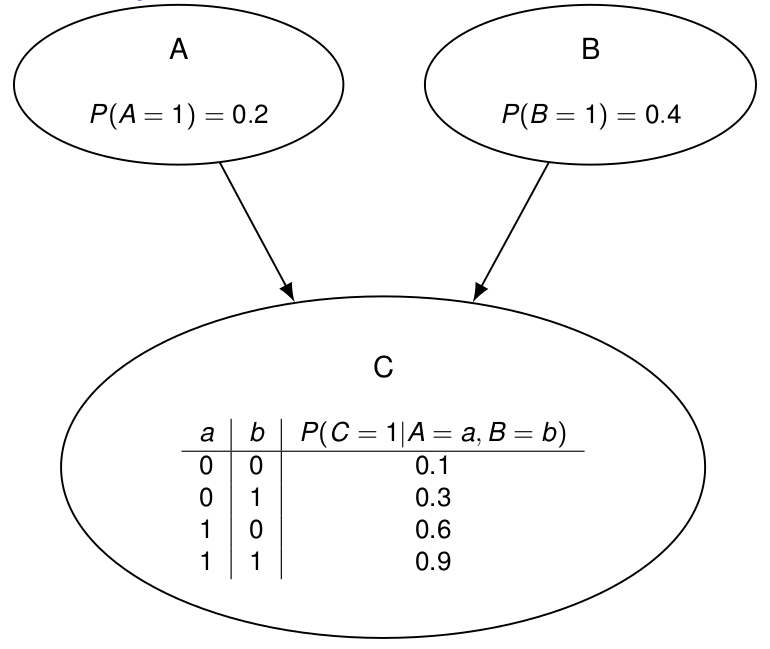Exemple d’un réseau en forme de V

Réseau en forme de V Ici, 6 nombres suffisent ici pour encoder la loi jointe de 3 variables binaires. Le calcul devient \begin{align*} P(A=0,B=1,C=1) &= P(C=1 | A = 0, B = 1) P(A=0) P(B=1) \\&= 0.3\times 0.8\times 0.4 = 0.288 \end{align*}

Exemple d’un réseau en étoile

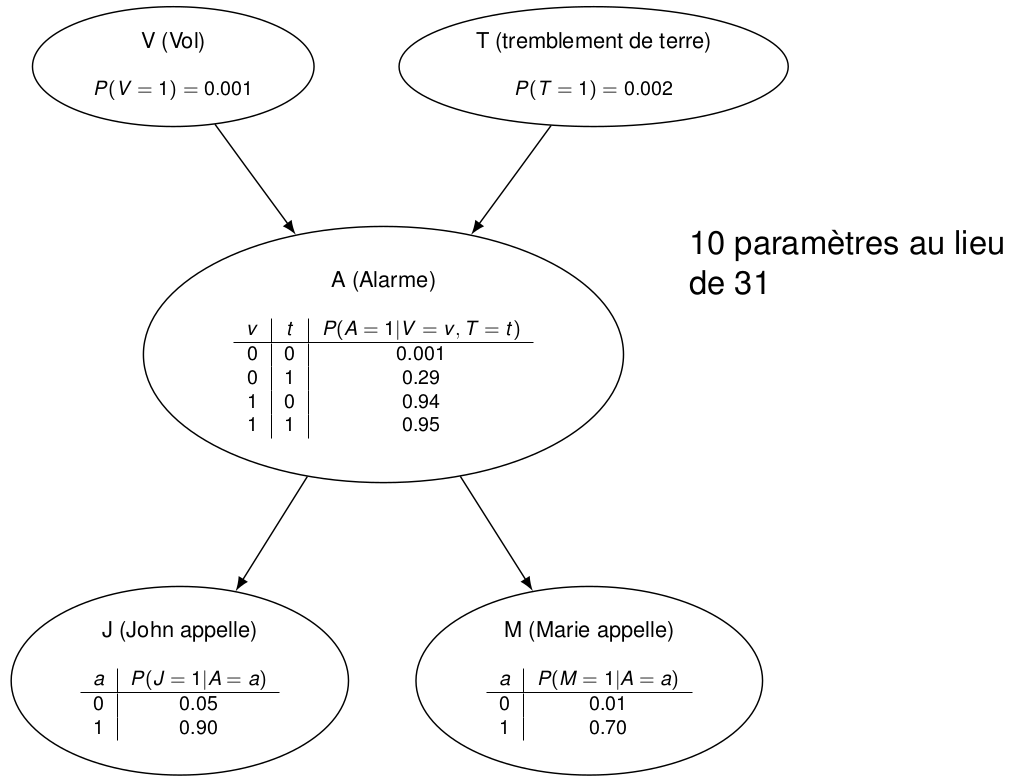
On modélise un système d’alarme avec les variables suivantes :

V : il y a un vol
T : il y a un tremblement de terre
A : l’alarme sonne
J : mon voisin m’appelle
M : une autre voisine m’appelle

Les voisins sont pris en compte car ils ont tendance à m’appeler plus souvent lorsque l’alarme sonne.

On peut aisément calculer la probabilité P(V=1,T=0,A=1,J=1,M=0 ) avec l’Équation 4.1 : \begin{align*} &P(V=1) P(T=0) P(A=1 | V=1, T=0)P(J=1|A=1) \\ & \times P(M=0|A=1) P(A=0,B=1,C=1)\\ &= P(C=1 | A = 0, B = 1) P(A=0) P(B=1) \\ &= 0.3\times 0.8\times 0.4 = 0.288 \end{align*}

4.3 Construction d’un réseau bayésien

Pour une loi jointe donnée, il existe plusieurs topologies de réseau possibles, certaines étant plus complexes et moins intuitives que d’autres. Le but est donc en général de construire le réseau le plus simple possible pour modéliser un problème donné.

Dans un réseau simple, les arcs modélisent les liens de cause à effet directs et les « racines » du graphe (qui n’ont pas de parents) correspondent aux causes premières (les événements qui semblent indépendants du reste).

La procédure pour obtenir une telle représentation est la suivante.

Ordonner les variables X_1, X_2, , X_n dans l’ordre des causes à effets.
Pour i=1,\dots,n :
1. ajouter un nœud pour la variable X_i ;
2. ajouter des arcs en provenance des parents(X_i) déjà présents dans le réseau en respectant les hypothèses d’indépendances conditionnelles : P(X_i=x_i | \boldsymbol{X}_{parents(X_i)} = \boldsymbol{x}_{parents(x_i)} ) = P(X_i = x_i | \boldsymbol{X}_{1:i-1} = \boldsymbol{x}_{1:i-1}) ;
3. remplir la table des probabilités conditionnelles de X_i (les valeurs de P(X_i=x_i | \boldsymbol{X}_{parents(X_i)} = \boldsymbol{x}_{parents(x_i)} ) pour tout \boldsymbol{x}_{parents(x_i)} )

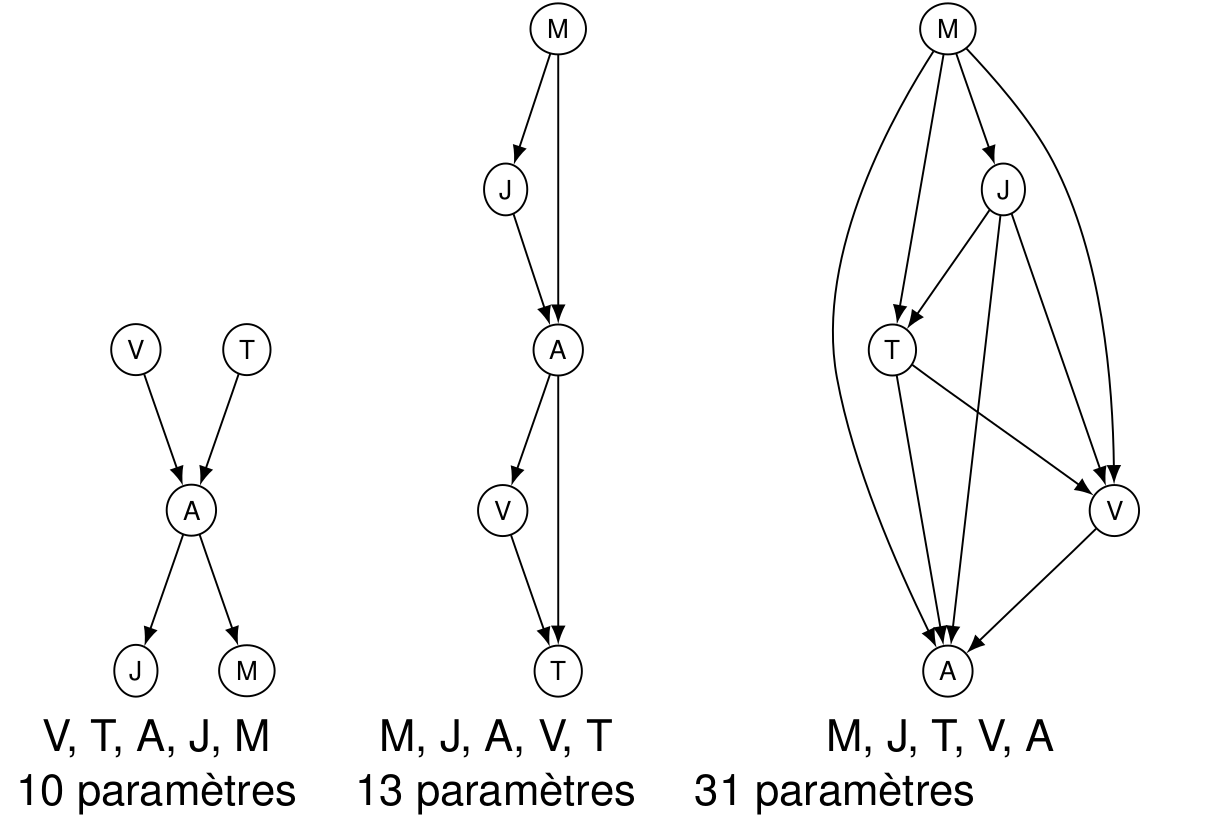
Reprenons l’exemple du réseau d’alarme, dans lequel la loi jointe sur 5 variables avait pu être encodée avec uniquement 10 paramètres. Ce réseau avait été obtenu par la procédure ci-dessus. Mais si nous inversons l’ordre des variables et l’appliquons, nous obtenons plus d’arcs et donc plus de paramètres.

Influence de l’ordre des variables sur la taille du réseau

Cela illustre aussi le problème des valeurs à entrer dans les tables : alors que celles-ci peuvent facilement être déterminées dans le réseau de gauche, les autres correspondent à des questions du type quelle est la probabilité que l’alarme sonne sachant que le voisin m’appelle et que la voisine ne m’appelle pas ?, dont la réponse est loin d’être évidente…

4.4 Analyse des liens d’indépendances conditionnelles

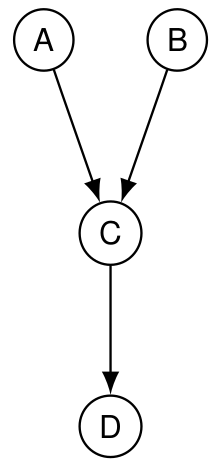
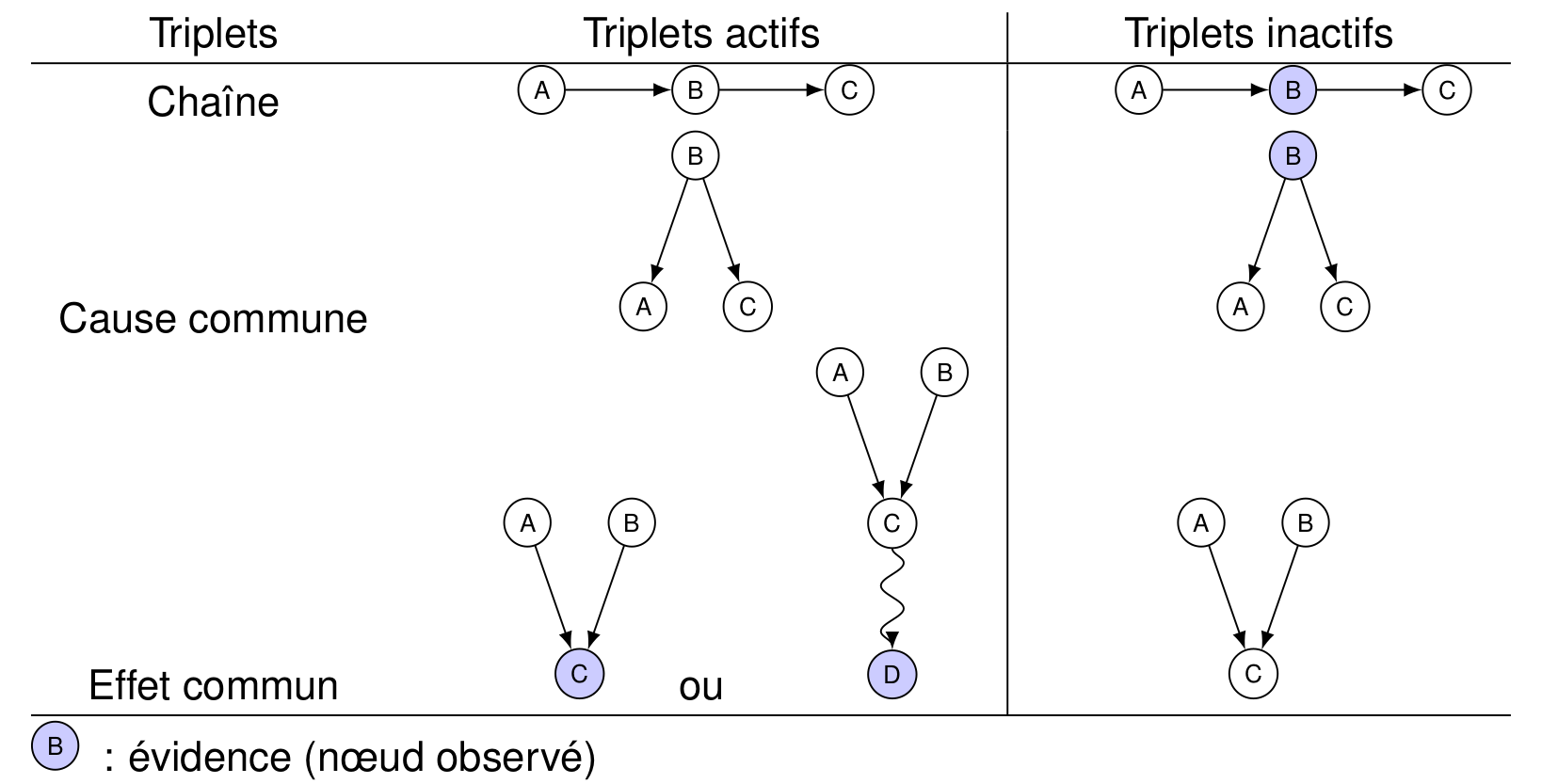
Etant donné un réseau bayésien, nous pouvons retrouver les liens de dépendance et d’indépendance entre les variables, grâce à la notion de d-séparation (séparation dans un graphe orienté).

Ici nous introduisons les notations suivantes :

A\perp B pour « A et B sont indépendantes » ;
A\perp B\ |\ C pour « A et B sont conditionnellement indépendantes sachant C ».

Ici la variable C (la partie à droite du sachant que) est appelée « évidence » : c’est l’ensemble des variables dont la valeur est connue / observée.

Pour déterminer si A\perp B\ |\ \boldsymbol{E}, il faut savoir si A et B sont d-séparées par \boldsymbol{E}. Nous allons étudier cela sur quelques exemples de triplets élémentaires, avant de généraliser.

4.4.1 Triplet en forme de chaîne de cause à effet

Ici,

A\not\perp B : A n’est pas indépendant de B car « A influence directement B » ;
A\not\perp C : A n’est pas indépendant de B car « A influence directement B qui influence C » ;
A\perp C\ | B : A est indépendant de C sachant B car toute l’influence de A sur C passe par B dont la valeur est fixée par l’observation.

Preuve d’indépendance

Pour prouver une indépendance, il suffit de montrer que la loi jointe est égale au produit des lois marginales : \begin{align*} P(A=a,C=c|B=b) &= \frac{P(A=a,B=b,C=c)}{P(B=b) }\\& = \frac{P(A=a)P(B=b|A=a)P(C=c|B=b) }{ P(B=b)} \\ &= P(A=a|B=b)P(C=c|B=b) \end{align*}

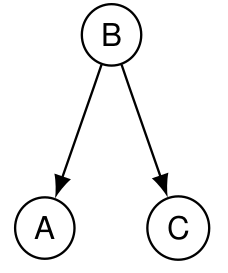
4.4.2 Triplet en forme de V inversé : cause commune

Ici,

A\not\perp C : A n’est pas indépendant de C car « A et C sont tous deux directement influencés par B » ;
A\perp C\ | B : A est indépendant de C sachant B car si la valeur de B est fixée, les probabilités de A sont entièrement déterminées et ne peuvent pas être modifiées par la valeur de C.

Preuve d’indépendance

Pour prouver une indépendance, il suffit de montrer que la loi jointe est égale au produit des lois marginales : \begin{align*} P(A=a,C=c|B=b) &= \frac{P(A=a,B=b,C=c)}{P(B=b) } \\&= \frac{P(A=a|B=b)P(B=b)P(C=c|B=b) }{ P(B=b)} \\&= P(A=a|B=b)P(C=c|B=b) \end{align*}

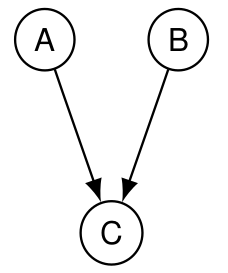
4.4.3 Triplet en forme de V : effet commun

Ici,

A\perp B : A est indépendant de B.

Preuve d’indépendance

Pour prouver une indépendance, il suffit de montrer que la loi jointe est égale au produit des lois marginales : \begin{align*} P(A=a,B=b) &= \sum_c P(A=a,B=b,C=c) \\& = P(A=a) P(B=b) \sum_c P(C=c|A=a, B=b) \\&= P(A=a) P(B=b) \end{align*}

A\not\perp B\ | C : A n’est pas indépendant de B sachant C car connaître la valeur de B modifie l’influence de A sur C, et inversement connaître la valeur de C crée un lien entre A et B.

Par exemple, si on constante une panne C qui peut avoir deux causes possibles A ou B, alors éliminer la cause B va augmenter la probabilité de la cause A.

Exemple illustratif avec A= j’ai gagné au loto, B= il fait beau, C= « je suis content » : si vous me voyez content, vous allez vous dire soit qu’il fait beau soit que j’ai gagné au loto. Mais si vous constatez ensuite qu’il pleut, cela va augmenter la probabilité avec laquelle j’ai gagné au loto : savoir que je suis content crée un lien de dépendance entre la météo et le résultat du loto.

4.4.4 Effect commun observé à distance

Reprenons le schéma précédent avec une variable supplémentaire :

Ici,

A\perp B : A est indépendant de B ;
A\not\perp B\ | C : A n’est pas indépendant de B sachant C ;
em A\not\perp B | D : A n’est pas indépendant de B sachant D car connaître la valeur de D revient à observer C à distance et nous donne de l’information sur sa valeur, et donc crée un lien entre A et B.

Pour l’exemple illustratif ci-dessus, imaginez D= « vous m’entendez chanter au loin ». Alors m’entendre chanter peut être suiffisant pour imaginer que je suis content et donc créer un lien statistique entre la météo et le loto dans votre tête.

4.4.5 Cas général

La méthode pour analyser les liens de dépendances dans le cas général repose sur l’étude des triplets élémentaires ci-dessus et résumée dans ce tableau :

La règle est la suivante :

X \perp Y \ | Z si et seulement si il n’existe pas de chemin (indépendamment de l’orientation des arcs) actif entre X et Y ;
un chemin est actif si tous les triplets qui le composent sont actifs.

4.5 Inférence

Un réseau bayésien encode une loi jointe et permet donc de calculer n’importe quelle probabilité impliquant n’importe quel sous-ensemble des variables. Cela s’appelle l’inférence.

Exemple d’inférence dans un réseau en forme de chaîne

Différents cas de figure :

P(B=1 | A=1)=0.6 \rightarrow lecture directe depuis la table
P(C=1 | A=1) ? Ici, il faut utiliser les règles de calcul sur les probabilités pour la reformuler en fonction des paramètres du réseau (c’est-à-dire les probabilités lisibles dans les tables) : \begin{align*} P(& C=1 | A=1) = P(C=1, B=0 | A=1) + P(C=1, B= 1 | A=1) \\&= P(C=1 | A=1, B=0)P(B=0|A=1) + P(C=1 | A=1, B=1)P(B=1|A=1)\\ &= P(C=1 | B=0)P(B=0|A=1) + P(C=1 | B=1)P(B=1|A=1)\end{align*} où nous avons utilisé la loi des probabilités totales, puis la factorisation de la loi jointe pour un couple.
P(A=1 | B=1) ? Ici, les variables sont inversées par rapport à l’ordre naturel du réseau. Pour inverser le conditionnement, nous utilisons la règle de Bayes, suivie de la loi des probabilités totales : \begin{align*} P(A=1 | B=1)&=\frac{P(B=1 | A=1)P(A=1)}{P(B=1}\\ &= \frac{P(B=1 | A=1)P(A=1)}{P(B=1 | A=1)P(A=1) + P(B=1 | A=0)P(A=0)} \end{align*}

Dans le cas général, nous pouvons utiliser les règles suivantes :

calcul d’une probabilité marginale avec la loi des probabilités totales : P(X=1) = \sum_{\boldsymbol{v}} P(X=1, \boldsymbol{V}=\boldsymbol{v})
calcul d’une probabilité conditionnelle P(X = 1 | \boldsymbol{E}=\boldsymbol{e}) :
- si parents(X)\subseteq \boldsymbol{E}\subseteq predecesseurs(X), alors lire la table des probabilités conditionnelles de X
- sinon, il y a d’autres variables \boldsymbol{V} et on passe par la loi jointe
  \begin{align*} P(X = 1 | \boldsymbol{E}=\boldsymbol{e}) &= \frac{P(X=1, \boldsymbol{E}=\boldsymbol{e})}{P(\boldsymbol{E}=\boldsymbol{e})}=\sum_{\boldsymbol{v}}\frac{ P(X = 1, \boldsymbol{V}=\boldsymbol{v}, \boldsymbol{E}=\boldsymbol{e}) }{P(\boldsymbol{E}=\boldsymbol{e})} \\ & = \sum_{\boldsymbol{v}} P(X = 1, \boldsymbol{V}=\boldsymbol{v} | \boldsymbol{E}=\boldsymbol{e}) \\ &= \sum_{\boldsymbol{v}} P(X = 1 |\boldsymbol{V}=\boldsymbol{v}, \boldsymbol{E}=\boldsymbol{e}) P(\boldsymbol{V}=\boldsymbol{v}|\boldsymbol{E}=\boldsymbol{e}) \end{align*}
calcul d’une probabilité conditionnelle en inversant la condition par la règle de Bayes : P(X = x | (\boldsymbol{E}_1, \boldsymbol{E}_2) = (\boldsymbol{e}_1, \boldsymbol{e}_2)) = \frac{P(\boldsymbol{E}_1=\boldsymbol{e}_1 | X=x, \boldsymbol{E}_2 = \boldsymbol{e}_2)P(X=x | \boldsymbol{E}_2 = \boldsymbol{e}_2)}{P(\boldsymbol{E}_1=\boldsymbol{e}_1 | \boldsymbol{E}_2 = \boldsymbol{e}_2)}

Exemple avec la réseau d’alarme

Reprenons l’exemple du réseau d’alarme pour calculer la probabilité que l’alarme sonne sachant que la voisine appelle et qu’il y a un vol : \begin{align*} P(A=1 | M=1, V=1) &= \frac{P(M=1 | A=1, V=1) P(A=1|V=1)}{P(M=1|V=1)}\\ &= \frac{P(M=1 | A=1) P(A=1|V=1)}{P(M=1|V=1)} \end{align*} où nous avons appliqué la règle de Bayes et l’indépendance conditionnelle M\perp V | A pour simplifier le numérateur.

Le dénominateur s’écrit \begin{align*} P(M=1|V=1) &= P(M=1| V=1,A=1)P(A=1|V=1) \\&\quad + P(M=1|V=1,A=0)P(A=0|V=1)\\ &= P(M=1| A=1)P(A=1|V=1) + P(M=1|A=0)P(A=0|V=1) \end{align*} et \begin{align*} P(A=1|V=1) &= P(A=1|V=1, T=0)P(T=0) + P(A=1|V=1, T=1)P(T=1)\\ P(A=0|V=1) &= 1 - P(A=1|V=1) \end{align*} ce qui permet de calculer le résultat à partir des paramètres du réseau.

4.6 Inférence approximative

L’inférence exacte discutée ci-dessus est en fait bien souvent trop complexe, dans le sens où le nombre d’additions et de multiplications peut croître rapidement, en particulier lorsque plusieurs chemins existent entre les variables.

Cependant, la plupart du temps un résultat exact n’est pas nécessaire. En effet, estimer une probabilité valant 0.2098456 à 0.21 peut se révéler suffisant pour beaucoup d’applications.

L’inférence approximativement cherche donc à estimer les probabiltés par simulation, c’est-à-dire à partir de tirages aléatoires des variables selon la loi jointe encodée par le réseau. En effet, une probabilité peut toujours s’exprimer comme l’espérance d’une indicatrice, elle-même pouvant s’estimer par une moyenne sur un certain nombre de tirages : P(\boldsymbol{X}= \boldsymbol{x}) = \mathbb{E}[\mathbf{1}(\boldsymbol{X}=\boldsymbol{x})] \approx \frac{\text{nb de tirages avec } \boldsymbol{X}=\boldsymbol{x}}{\text{nb total de tirages}} Pour pouvoir simuler des tirages selon la bonne loi de probabilité, il faut

commencer par tirer les variables dans les racines du graphe (les nœuds sans parents) dont les probabilités sont données indépendamment des autres variables ;
suivre les arcs pour propager les valeurs tirées et connaître le conditionnement des variables suivantes.

Exemple de simulation avec un réseau bayésien

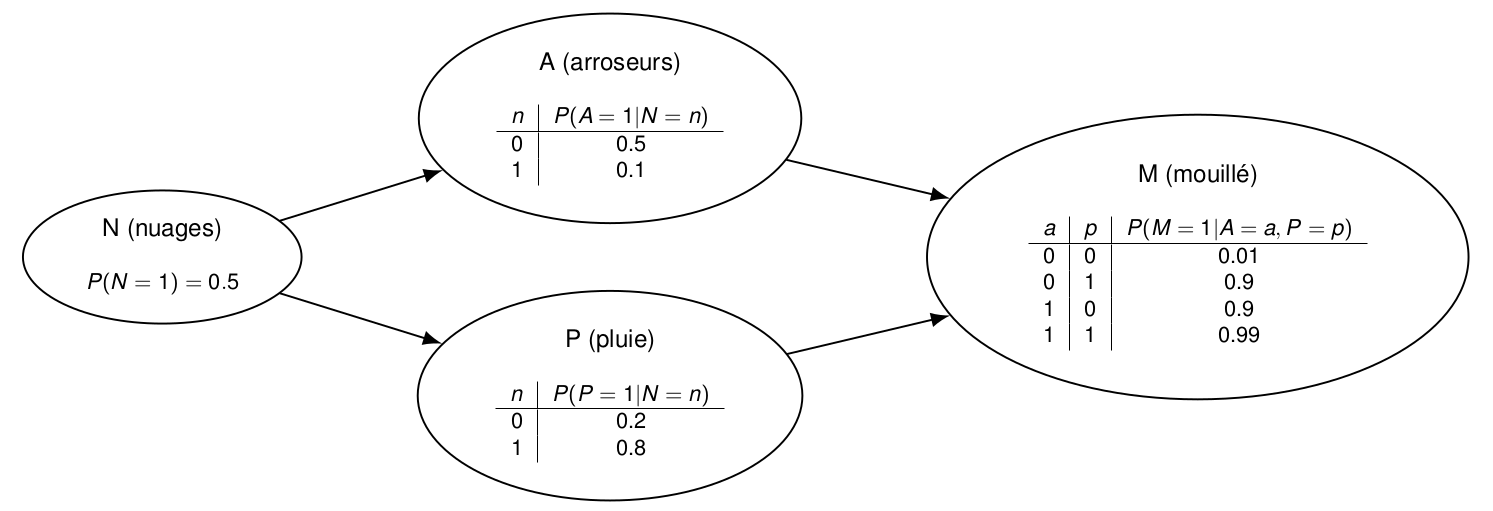
Considérons 4 variables modélisant la météo et l’humidité de l’herbe :

Pour estimer P(N=1, A=0, P=1,M=1), nous générons des tirages en commençant par la valeur binaire n de N avec P(N=1)=0.5. Cette valeur n est ensuite utilisée pour fixer les lois de probabilité de A et P à utiliser pour tirer ces variables : P(A=1|N=n) et P(P=1|N=n). Enfin, la valeur de M est tirée avec une probabilité d’avoir 1 fixée par les valeurs de a et p.

4.6.1 Estimation des probabilités conditionnelles

Pour une probabilité conditionnelle, nous utilisons la définition : \begin{align*} P(X= x | \boldsymbol{E}=\boldsymbol{e}) &= \frac{P(X= x ,\boldsymbol{E}=\boldsymbol{e})}{P(\boldsymbol{E}=\boldsymbol{e})} \approx \frac{\frac{\text{nb de tirages avec} X=x \ et\ \boldsymbol{E}=\boldsymbol{e}}{\text{nb tirages total}}}{\frac{\text{nb de tirages avec } \boldsymbol{E}=\boldsymbol{e}}{\text{nb tirages total}}} \\ &\approx \frac{\text{nb de tirages avec} X=x \ et\ \boldsymbol{E}=\boldsymbol{e}}{\text{nb de tirages avec } \boldsymbol{E}=\boldsymbol{e}} \end{align*}

4.6.2 Pondération par la vraisemblance

L’estimation ci-dessus pose un souci lorsque la condition \boldsymbol{E}=\boldsymbol{e} fait référence à un événement rare. Dans ce cas, la plupart des tirages seront jetés à la poubelle avant de calculer la probabilité qui sera au final estimée réellement qu’à partir de très peu de données.

Pour éviter ce souci, la pondération par la vraisemblance applique les modifications suivantes :

à chaque tirage i, les valeurs \boldsymbol{E}=\boldsymbol{e} sont forcées et non aléatoires (ce qui implique que tous les tirages sont retenus dans le calcul) ;
la vraisemblance de chaque tirage v_i est mémorisée : elle est donnée par le produit des probabilités conditionnelles des valeurs forcées et correspond à la probabilité que ce tirage des variables forcées soit réellement issu de la loi jointe encodée par le réseau ;
l’estimation est corrigée ainsi : P(X= x | \boldsymbol{E}=\boldsymbol{e})\approx \frac{\sum_i v_i \mathbf{1}(X=x)}{\sum_i v_i}
où chaque tirage est pondéré par sa vraisemblance.