def kmeans(X, K):
m, d = X.shape
C = np.min(X) + (np.random.rand(K,d) * (np.max(X)-np.min(X)))
Cprecedent = np.zeros(C.shape)
Distances = np.zeros((m,K))
history = []
while np.linalg.norm(C - Cprecedent) > 1e-6:
Cprecedent = np.copy(C)
# Classer les données:
for k in range(K):
Distances[:,k] = np.linalg.norm(X-C[k,:], axis=1)
y = np.argmin(Distances, axis=1)
history.append([np.copy(y),np.copy(C)])
# Mettre à jour les centres
for k in range(K):
C[k,:] = np.mean(X[y==k,:], axis=0)
return y, C, history
#### Test ###
X = np.random.rand(100,2)
y = np.random.rand(100) > 0.5
X[y,:] += np.array([2,2])
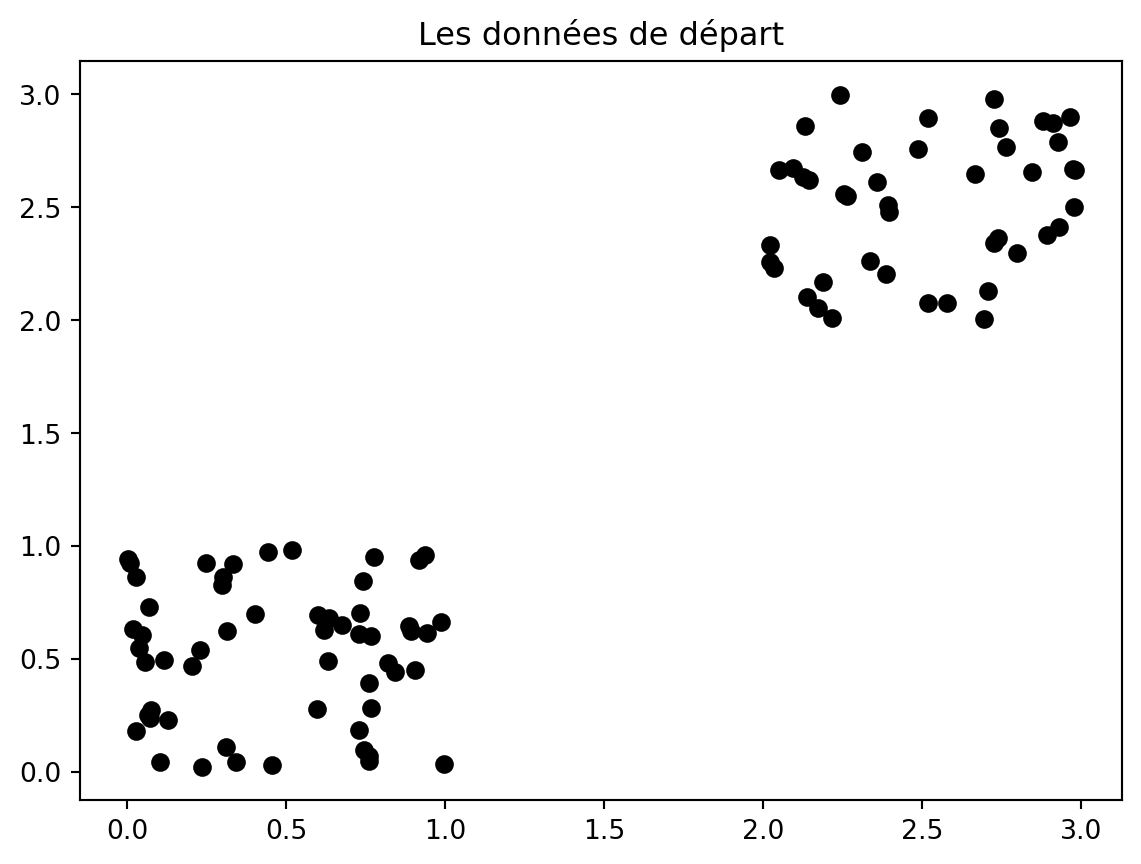
plt.plot(X[:,0], X[:,1], "ok")
plt.title("Les données de départ")
ypred, C, history = kmeans(X, 2)
plt.figure()
plt.plot(X[ypred==0,0], X[ypred==0,1], 'ob', alpha=0.5)
plt.plot(X[ypred==1,0], X[ypred==1,1], 'or', alpha=0.5)
plt.plot(C[0,0], C[0,1], "*b", markersize=20)
plt.plot(C[1,0], C[1,1], "*r", markersize=20)
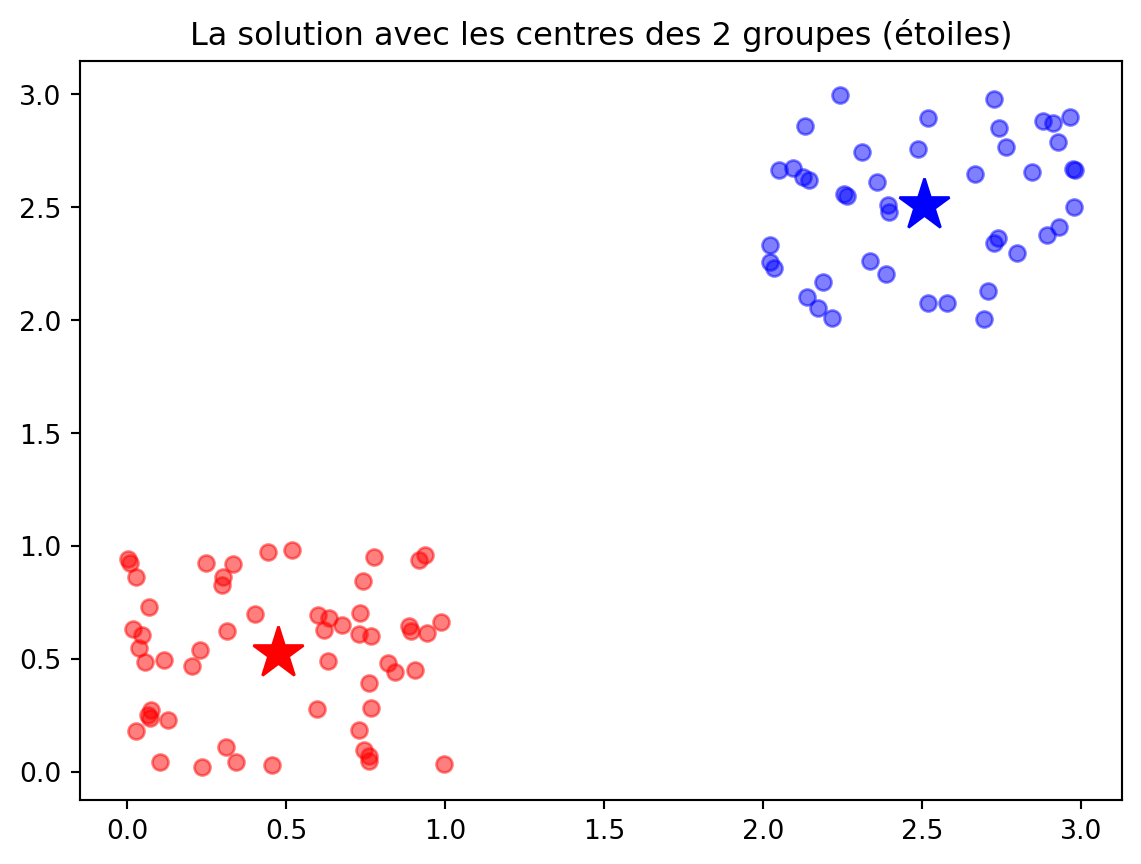
plt.title("La solution avec les centres des 2 groupes (étoiles)")
for t in range(len(history)):
ypred, C = history[t]
plt.figure()
plt.plot(X[ypred==0,0], X[ypred==0,1], 'ob', alpha=0.5)
plt.plot(X[ypred==1,0], X[ypred==1,1], 'or', alpha=0.5)
plt.plot(C[0,0], C[0,1], "*b", markersize=20)
plt.plot(C[1,0], C[1,1], "*r", markersize=20)
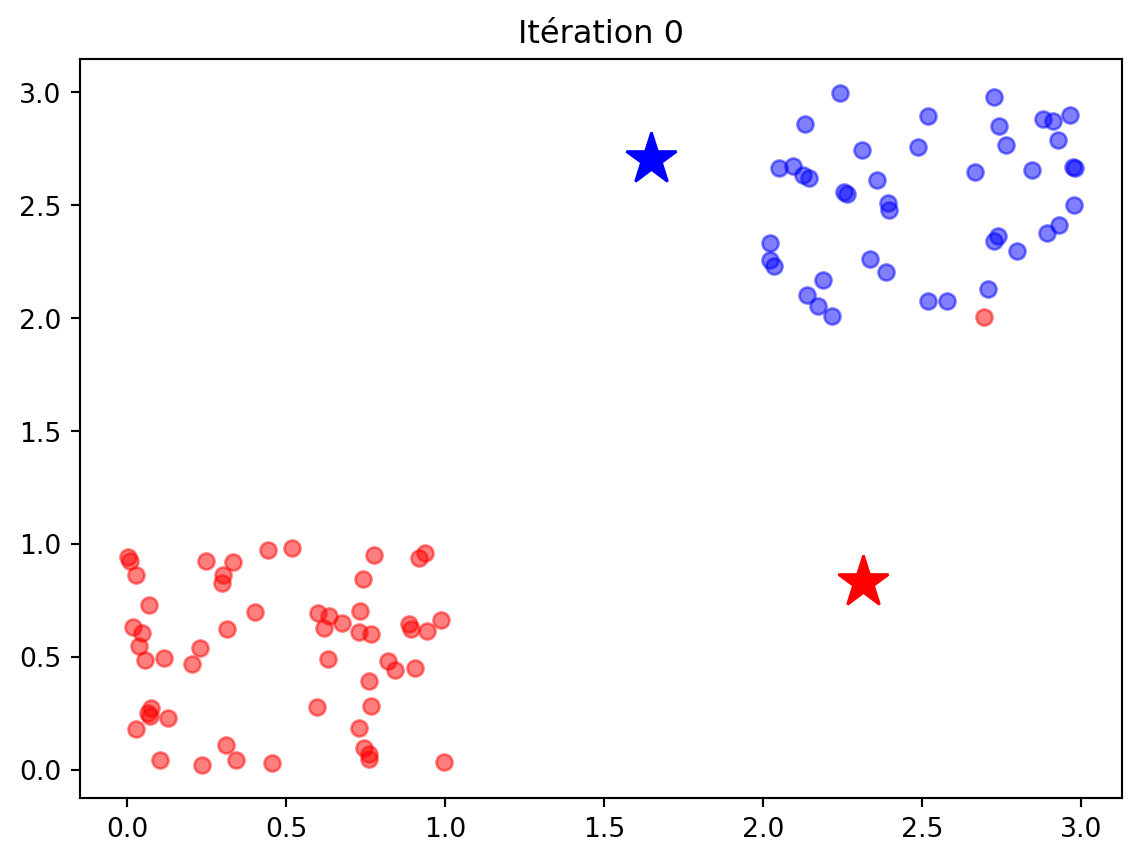
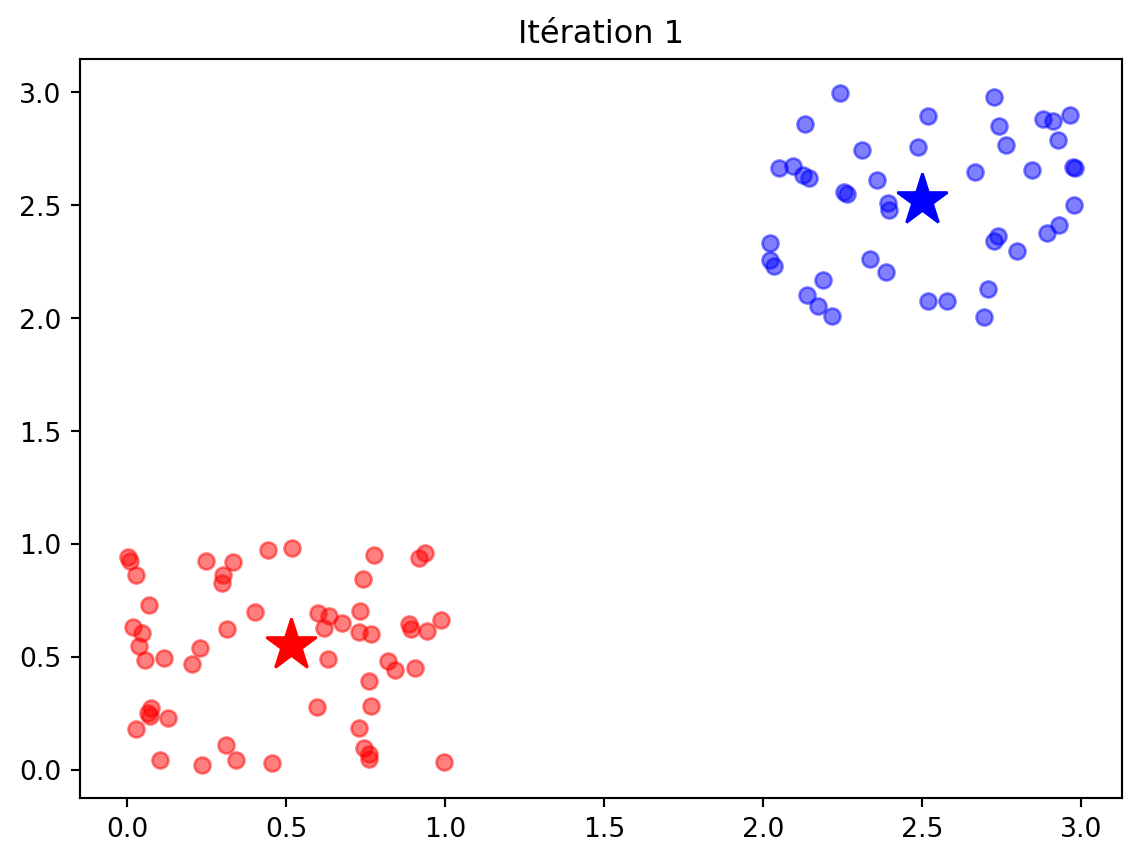
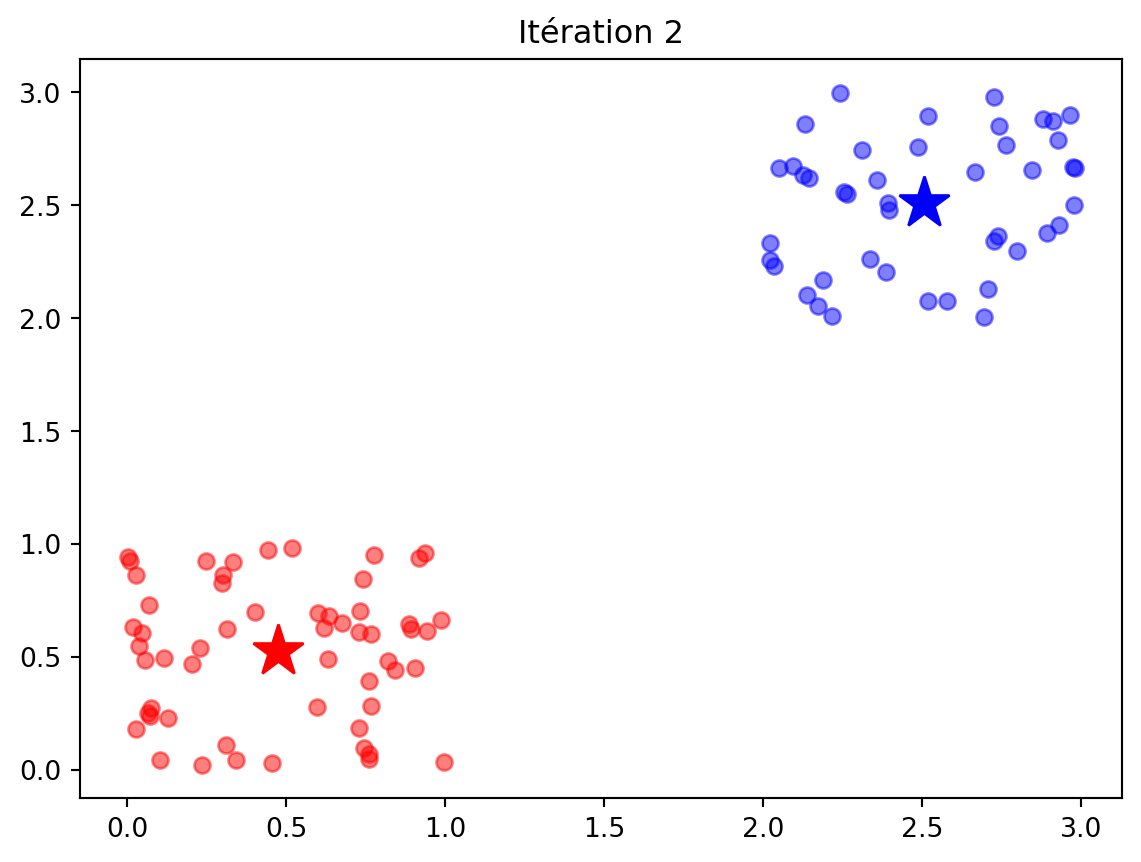
plt.title("Itération " + str(t))23 Algorithme K-means
L’algortihme K-means est un algorithme de clustering. À partir d’un ensemble d’exemples non étiquetés S = \{\boldsymbol{x}_1, \dots, \boldsymbol{x}_m\} il va trouver une répartition de ceux-ci en K groupes G_k, k=1,\dots, K, mais aussi les prototypes de ces groupes, c’est-à-dire des exemples (artificiels) et représentatifs des données de chaque groupe. Ces prototypes correspondent en fait simplement aux centres des groupes \boldsymbol{c}_k.
23.1 Détails de l’algorithme
- Initialiser les K centres c_k des groupes (typiquement aléatoirement)
- Classer les exemples avec y_i = \arg\min_{k\in\{1,\dots, K\}} \|\boldsymbol{x}_i - \boldsymbol{c}_k\| \tag{23.1} G_k = \{i : y_i = k\}
- Mettre à jour les centres des groupes avec \boldsymbol{c}_k = \frac{1}{|G_k|} \sum_{\boldsymbol{x}_i\in G_k} \boldsymbol{x}_i \tag{23.2} où |G_k| désigne le cardinal du groupe G_k (le nombre d’exemples affectés à ce groupe).
- Répéter depuis 2. jusqu’à convergence.
Pour être complet, l’algorithme devrait inclure la gestion des cas où aucun point n’est affecté à un groupe. Typiquement, il est possible de réinitialiser le centre du groupe aléatoirement ou de supprimer complétement le groupe du reste de la procédure.
23.2 Critère optimisé par K-means
L’algorithme K-means est une méthode d’optimisation alternée pour minimiser le critère J((\boldsymbol{c}_k)_{k=1}^K, (G_k)_{k=1}^K) = \sum_{k=1}^K \sum_{i\in G_k} \|\boldsymbol{x}_i - \boldsymbol{c}_k\|^2 qui mesure la somme de toutes les distances des points \boldsymbol{x}_i au centre \boldsymbol{c}_k du groupe G_k auquel il est affecté.
L’algorithme alterne en fait entre
- la minimisation de cette fonction par rapport aux groupes G_k (à centres fixés),
- puis la minimisation par rapport aux centres \boldsymbol{c}_k (à groupes G_k fixés).
Il est aisé de voir que, pour minimiser ce critère, il est nécessaire d’affecter chaque point \boldsymbol{x}_i au centre \boldsymbol{c}_k le plus proche, ce qui donne la formule de classification Équation 23.1.
Pour minimiser par rapport aux centres, on remarque que le critère est une somme de K termes, chacun n’impliquant qu’un centre \boldsymbol{c}_k de manière indépendante. Il suffit donc de résoudre les K sous-problèmes d’optimisation \min_{\boldsymbol{c}_k} J_k(\boldsymbol{c}_k),\qquad J_k(\boldsymbol{c}_k) = \sum_{i\in G_k} \|\boldsymbol{x}_i - \boldsymbol{c}_k\|^2 Le gradient de l’objectif J_k(\boldsymbol{c}_k) est ici \frac{\text{d} J_k(\boldsymbol{c}_k)}{\text{d} \boldsymbol{c}_k} = - 2 \sum_{i\in G_k} (\boldsymbol{x}_i - \boldsymbol{c}_k) et la solution est obtenue lorsque ce gradient est nul, ce qui donne |G_k| \boldsymbol{c}_k = \sum_{i\in G_k} \boldsymbol{x}_i et la formule Équation 23.2 qui calcule \boldsymbol{c}_k comme la moyenne des points.
On peut montrer qu’à chaque itération de l’algorithme, le critère J((\boldsymbol{c}_k)_{k=1}^K, (G_k)_{k=1}^K) décroît de manière monotone. Cependant, aucune garantie n’est donnée sur l’optimalité de la solution, car la solution converge vers un point qui dépend fortement de l’initialisation.
def J(C, y):
cost = 0
for k in range(len(C)):
cost += np.sum( ( X[y==k,:] - C[k,:] )**2 )
return cost
# Données en grande dimension
m = 200
d = 20
K = 5
X = np.random.randn(m,d)
y = np.random.randint(0,K,size=m)
Copt = np.zeros((K,d))
for k in range(K):
X[y==k,:] += 3 * k * np.ones(d)/np.sqrt(d)
Copt[k,:] = np.mean(X[y==k,:],0)
print("Coût optimal =", J(Copt,y))
ypred, C, _ = kmeans(X, K)
print("Coût de la solution K-means =", J(C,ypred))Coût optimal = 3858.100221643007
Coût de la solution K-means = 3919.281232465867623.3 Amélioration par multiples initialisations
Pour améliorer la qualité de la solution, une approche simple consiste à répéter l’algorithme N fois à partir d’initialisation aléatoires et différentes pour ne conserver au final que la solution associée à la plus petite valeur de J((\boldsymbol{c}_k)_{k=1}^K, (G_k)_{k=1}^K).
Cependant, le nombre d’initialisations requis croît rapidement avec la dimension du problème, comme prédit par la malédiction de la dimension.
23.4 K-means++ : initialisation dispersée
L’algorithme K-means++, proposé par Arthur et Vassilvitskii (2007), fournit une initialisation particulièrement efficace pour K-means. Celle-ci repose sur l’idée que les résultats de K-means sont meilleurs lorsque les centres initiaux sont bien dispersés dans l’espace.
K-means++ choisi les centres initiaux parmi les m points \boldsymbol{x}_i de la base d’apprentissage ainsi :
- Tirer \boldsymbol{c}_1 aléatoirement de manière uniforme parmi tous les exemples \boldsymbol{x}_i, i=1,\dots, m.
- Pour k=2,\dots,K :
- Pour chaque point \boldsymbol{x}_i, calculer la distance au centre le plus proche D_i = \min_{1\leq j< k} \|\boldsymbol{x}_i - \boldsymbol{c}_k\|
- Choisir \boldsymbol{c}_k aléatoirement selon la loi de probabilité P(\boldsymbol{c}_k=\boldsymbol{x}_i) = \frac{D_i^2}{ \sum_{i} D_i^2}