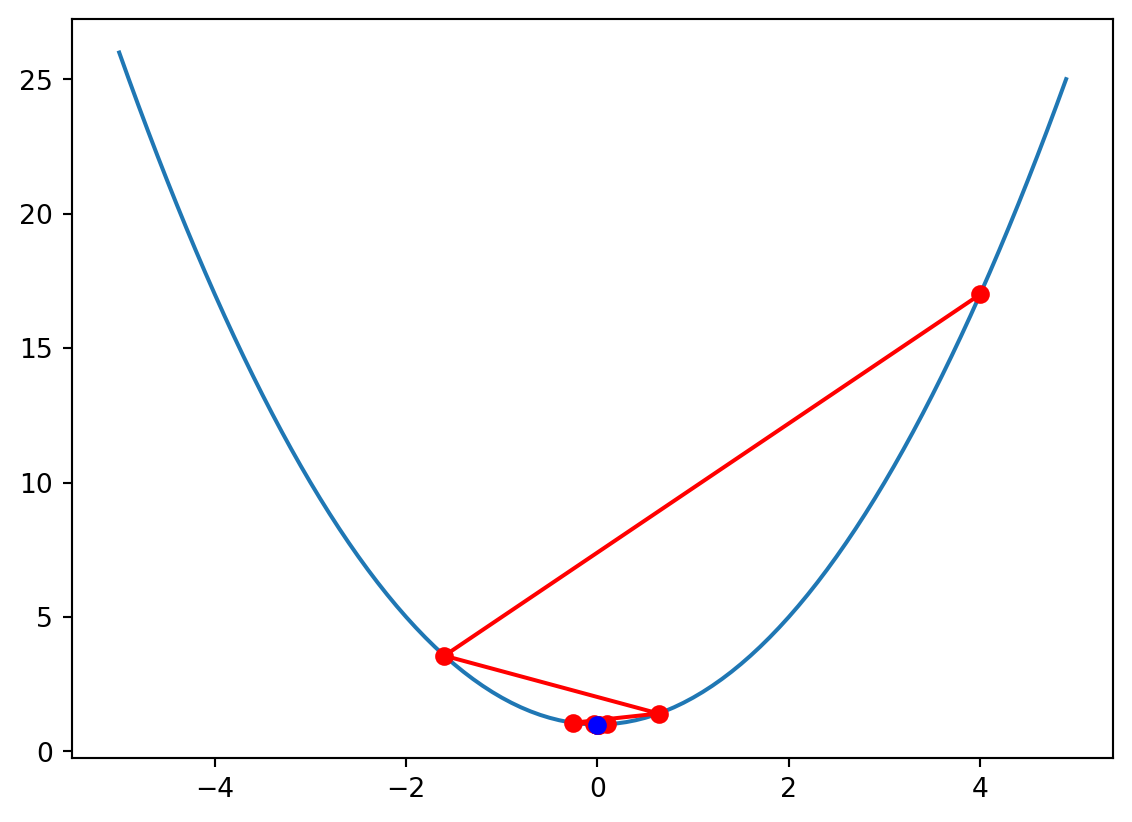
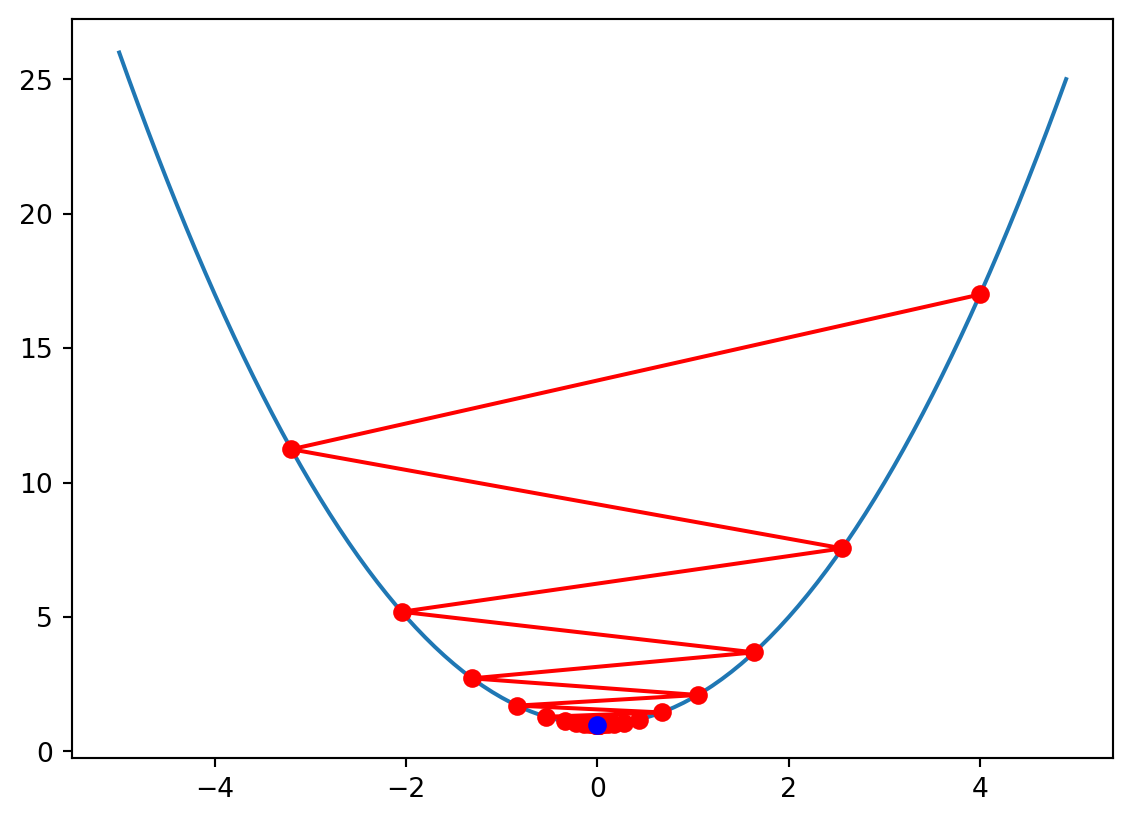
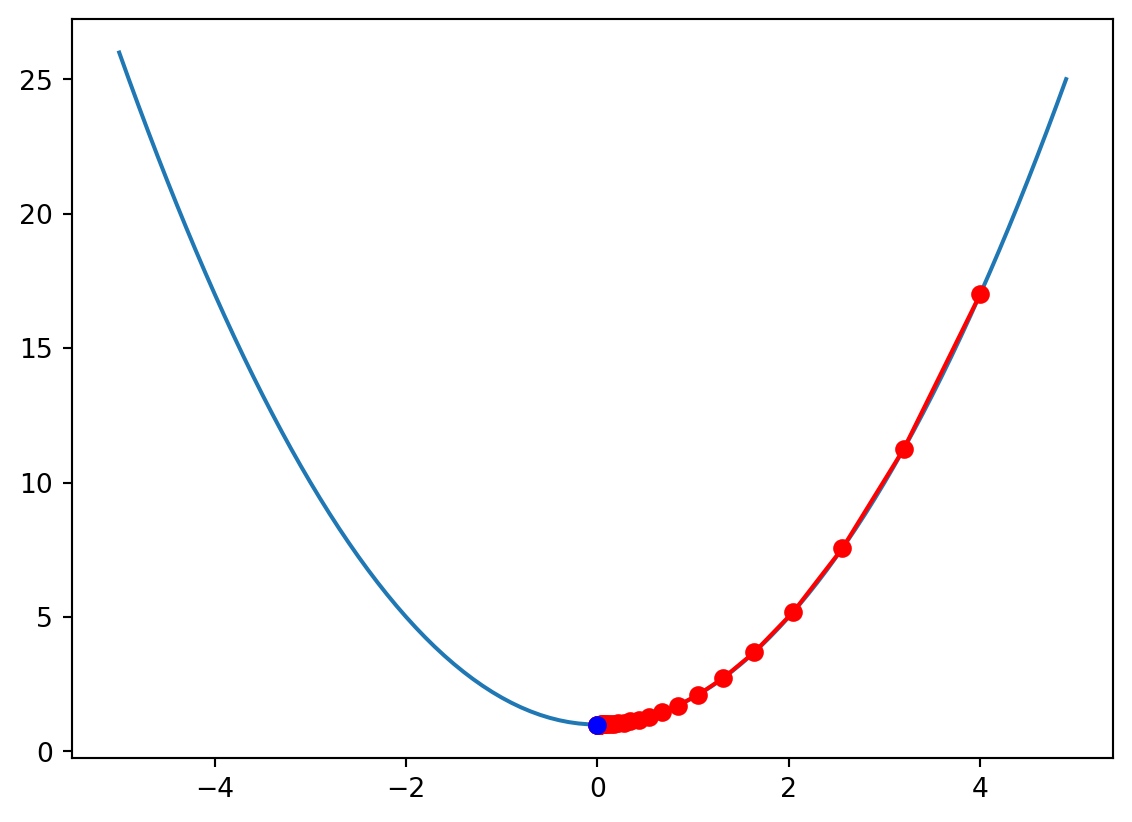
x = 4.00000, f(x) = 17.00000, df_df(x) = 8.00000
x = -3.20000, f(x) = 11.24000, df_df(x) = -6.40000
x = 2.56000, f(x) = 7.55360, df_df(x) = 5.12000
x = -2.04800, f(x) = 5.19430, df_df(x) = -4.09600
x = 1.63840, f(x) = 3.68435, df_df(x) = 3.27680
x = -1.31072, f(x) = 2.71799, df_df(x) = -2.62144
x = 1.04858, f(x) = 2.09951, df_df(x) = 2.09715
x = -0.83886, f(x) = 1.70369, df_df(x) = -1.67772
x = 0.67109, f(x) = 1.45036, df_df(x) = 1.34218
x = -0.53687, f(x) = 1.28823, df_df(x) = -1.07374
x = 0.42950, f(x) = 1.18447, df_df(x) = 0.85899
x = -0.34360, f(x) = 1.11806, df_df(x) = -0.68719
x = 0.27488, f(x) = 1.07556, df_df(x) = 0.54976
x = -0.21990, f(x) = 1.04836, df_df(x) = -0.43980
x = 0.17592, f(x) = 1.03095, df_df(x) = 0.35184
x = -0.14074, f(x) = 1.01981, df_df(x) = -0.28147
x = 0.11259, f(x) = 1.01268, df_df(x) = 0.22518
x = -0.09007, f(x) = 1.00811, df_df(x) = -0.18014
x = 0.07206, f(x) = 1.00519, df_df(x) = 0.14412
x = -0.05765, f(x) = 1.00332, df_df(x) = -0.11529
x = 0.04612, f(x) = 1.00213, df_df(x) = 0.09223
x = -0.03689, f(x) = 1.00136, df_df(x) = -0.07379
x = 0.02951, f(x) = 1.00087, df_df(x) = 0.05903
x = -0.02361, f(x) = 1.00056, df_df(x) = -0.04722
x = 0.01889, f(x) = 1.00036, df_df(x) = 0.03778
x = -0.01511, f(x) = 1.00023, df_df(x) = -0.03022
x = 0.01209, f(x) = 1.00015, df_df(x) = 0.02418
x = -0.00967, f(x) = 1.00009, df_df(x) = -0.01934
x = 0.00774, f(x) = 1.00006, df_df(x) = 0.01547
x = -0.00619, f(x) = 1.00004, df_df(x) = -0.01238
x = 0.00495, f(x) = 1.00002, df_df(x) = 0.00990
x = -0.00396, f(x) = 1.00002, df_df(x) = -0.00792
x = 0.00317, f(x) = 1.00001, df_df(x) = 0.00634
x = -0.00254, f(x) = 1.00001, df_df(x) = -0.00507
x = 0.00203, f(x) = 1.00000, df_df(x) = 0.00406
x = -0.00162, f(x) = 1.00000, df_df(x) = -0.00325
x = 0.00130, f(x) = 1.00000, df_df(x) = 0.00260
x = -0.00104, f(x) = 1.00000, df_df(x) = -0.00208
x = 0.00083, f(x) = 1.00000, df_df(x) = 0.00166
x = -0.00066, f(x) = 1.00000, df_df(x) = -0.00133
x = 0.00053, f(x) = 1.00000, df_df(x) = 0.00106
x = -0.00043, f(x) = 1.00000, df_df(x) = -0.00085